ここまでで、化学反応の反応物と生成物のギブズエネルギーの差の符号から反応の自発性が分かると述べてきたが、ここで見ているΔGの値はあくまで100%の反応物と100%の生成物のギブズエネルギーの差であり、いわば反応物と生成物が混合が起きない場合の進行方向である。ところが実際には、反応が進むに従って反応物が減少して生成物が増加する物質量変化がある上に、反応の途中では反応物と生成物が混ざっているので混合によるエントロピー変化もある。従って物質量変化・混合によるギブズエネルギーの変化は、反応物・生成物100%のギブズエネルギーに比率を掛けるだけで単純計算できるわけではない。結果として、反応物と生成物が混合された系のギブズエネルギーには反応が100%進行する前に極小値があり、反応はここで停止する。これが化学平衡である。同様に液体と気体の間にも相平衡がある。
物質量変化と気体のギブズエネルギー
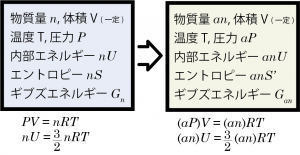
化学反応が起きると系の各成分の物質量が変化するので、平衡について考える前に、まずは物質量変化に伴うギブズエネルギー変化を計算してみることにしよう。ここでは理想気体を想定して、ある体積、温度の容器内で気体Aが n モルあるときのギブズエネルギーを Gn と書くことにして、同じ容器に同じ気体が an モルあるときギブズエネルギーをどのように表すことができるかを考える。
気体Aの体積、温度は一定として系の体積を V , 圧力を P , 温度を T 、また気体の内部エネルギーを nU , エントロピーを nS と書くことにすると*1この系における1モルあたりの内部エネルギー、エントロピーを U, S とする。、この系では PV=nRT という状態方程式が成立している。この時の系のギブズエネルギー Gn を定義を元に計算すると、Gn=nU+PV-TnS である。
次に、容器内の気体Aの一部を取り除き、体積 V, 温度 T は変わらず物質量のみ an モルになった系を考えると、状態方程式から内部の圧力は aP , 内部エネルギー anU である。このとき、系の圧力が変わっているということは,モルエントロピーの値も元の S とは異なる値になるはずである。そこで、物質量が変化した新しい系における気体Aのモルエントロピーを S’ と書くことにすれば、物質量 an モル分のエントロピーは anS’ と書ける。
ここで、この新しい系と同じ圧力 aP ・温度 T の気体Aを1モル用意したとすると、その体積は V/a である*2状態方程式PV=nRTより。。エントロピーの大きさは系の大きさに比例するので*3系の大きさをa倍すると、状態変数の大きさもa倍されるような性質を示量性と呼ぶ。7.1ギブズエネルギーにも記載したように物質量n, 体積V, 内部エネルギーU, エントロピーS, エンタルピーH, ギブズエネルギーG, ヘルムホルツエネルギーA は示量性を持つ。一方、圧力Pや温度Tにはこのような性質はない。、1モルの気体Aが入った圧力 aP ・体積 V/a ・エントロピー S’ の系を an 倍したものが新しい系ということになる。
2つの状態におけるモルエントロピーS, S’ の差というのは(P,V)→(aP,V⁄a) に定温可逆過程で変化する際のエントロピー変化を計算することができる。つまり、等温可逆過程の体積変化のエントロピー変化 ![]() の関係式から、S’ は$$S’=S+R ln \left(\frac{P}{aP}\right)$$ となる。
の関係式から、S’ は$$S’=S+R ln \left(\frac{P}{aP}\right)$$ となる。
ここで得られた値をギブズエネルギーの定義式に代入することで、物質量が an となった新しい系のギブズエネルギーは
$$G_{an}=anU+aPV-Tan\left(S+Rln\left(\frac{P}{aP}\right)\right)=aG_n-anRTln(\frac{1}{a})$$となる。
つまり、化学反応によって物質量が n から an になったことによるギブズエネルギー変化は、元のギブズエネルギー Gn に物質量の増加・減少割合 a を掛けただけではないことがわかる。
化学平衡と化学ポテンシャル
高校の化学の教科書では、化学反応の反応速度が反応式の左→右と、右→左で等しく、各成分の比率が一定に保たれて見かけ上反応が止まって見えるような状況を化学平衡の状態といった。また化学反応$$aA+bB+…\rightleftharpoons xX+yY+…$$という化学反応があったとき、化学平衡において各成分の組成を決めるのが平衡定数であり、$$K=\frac{[X]^x[Y]^y…}{[A]^a[B]^b…}$$で表された。ところが、この平衡定数の値がどのように出てきたものか、反応熱等と関係あるのかないのかについては出てこなかったと思う。ところが今回、熱力学で出てきたギブズエネルギーを使うと、この平衡定数を決めることができるようになる。
ここまで見てきたとおり、熱力学では系のギブズエネルギーは反応物と生成物のギブズエネルギーの和で表される。ただし、混合エントロピーの影響があるため、反応物と生成物が共存する時のギブズエネルギーはそれぞれが100%のときのエネルギーを直線的に繋いだ値にはならず、上の図のように、反応が進行するに従って下に凸の曲線状に推移する。ここで、ギブズエネルギーが極小となる組成に到達した後は、生成物が多い組成、反応物が多い組成のどちらの組成に移動しても ΔG > 0 となってしまい、反応は進行できない。つまり、化学反応はギブズエネルギーが極小となる組成にて化学平衡に達することになる。
ギブズエネルギーが極小となる組成では、生成物のギブズエネルギーの増加率と反応物のギブズエネルギーの減少率が釣り合っていると考えることができる。これを表す式が
である。ここで出てきたギブズエネルギーの物質量変化に対する増加率、すなわちギブズエネルギーを物質量で偏微分した値 ![]() は化学ポテンシャルと呼ばれる。
は化学ポテンシャルと呼ばれる。
例えば液体−気体が共存している状態における相平衡状態なら ![]() が成立している。
が成立している。
2成分系均一気相反応
次に、2成分系の化学反応についてのギブズエネルギー変化を考えてみよう。2成分系の反応は ![]() で表される。*4今回の話は2成分とも気体で反応が起きることを想定している。いす形←→船形のシクロヘキサンの2つの立体配座間の構造変化を想像すると良いかもしれない。ノルマルブタン(CH3CH2CH2CH3)とイソブタン(CH3CH(CH3)2)の異性化も反応物と生成物による化学反応式としてはこのように書くことができるだろう。
で表される。*4今回の話は2成分とも気体で反応が起きることを想定している。いす形←→船形のシクロヘキサンの2つの立体配座間の構造変化を想像すると良いかもしれない。ノルマルブタン(CH3CH2CH2CH3)とイソブタン(CH3CH(CH3)2)の異性化も反応物と生成物による化学反応式としてはこのように書くことができるだろう。
さて、この系で反応前に成分Aが n モルあり、また圧力 P , 温度 T が一定だったとする。この反応では反応しても物質量の合計が変わらないので理想気体を想定すれば体積 V も一定である。このとき、反応前は反応物Aのみがこの系の中に n モルあるので、系のギブズエネルギーは nGA である、また、反応が完全に進行して生成物Bのみになった場合は、ギブズエネルギーは nGB である。このとき1モルあたりのモル反応ギブズエネルギーは ∆r G=GB-GA となる。さて、反応が進行して系の中に成分AがnAモル、成分BがnBモルになったときのことを考える(nA+nB=n )。
このとき、成分Aのギブズエネルギーは$$n_A G’_A=n_A G_A-n_A RTln(\frac{(n_A+n_B)P}{n_A P})$$となり、成分Bのギブズエネルギーは$$n_B G’_B=n_B G_B-n_B RTln(\frac{(n_A+n_B)P}{n_B P})$$となる。さらに、系全体のギブズエネルギーは$$G’_{all}=n_A G’_A+n_B G’_B=n_A G_A+n_B G_B+n_A RTln(\frac{n_A}{n_A+n_B })+n_B RTln(\frac{n_B}{n_A+n_B })$$となる。
なお、成分A、Bの物質量がそれぞれ nA モル、nB モルになったときの成分Aのモルギブズエネルギーを G’A 、成分Bのモルギブズエネルギーを G’B 、系全体のギブズエネルギーを G’all とした。
さて、平衡状態では、nA, nB のどちらが増加・減少しても、G’all が大きくなってしまうため、
$$\frac{\partial G’_{all}}{\partial n_A }=\frac{\partial G’_{all}}{\partial n_B }$$になっているはずである。そこで実際にこの偏微分を計算してみると、$$G_A+RTln(\frac{n_A}{n})=G_B+RTln(\frac{n_B}{n})$$ となり、さらに変形すると、$$G_B-G_A=-RTln(\frac{n_B}{n_A} )$$となる。
この反応のモル反応ギブズエネルギーは$$∆_r G=G_B-G_A$$ 物質量の比は圧平衡定数と等しく$$\frac{n_B}{n_A} =\frac{P_B}{P_A} =K_p$$となるので、最終的に$$\Delta_r G=-RTlnK_p$$となる。
つまり、平衡定数、すなわち化学平衡になったときの組成についてもギブズエネルギーから計算できることになるとともに、平衡定数からギブズエネルギーを求めることもできるということである。
より成分が多い多成分系においても、平衡定数とギブズエネルギーは同様の関係がある。
ここまでみてきたように、エントロピーやエンタルピー、ギブズエネルギーといった新しい物理量を使うことで、高校の化学では天下り的に出てきた平衡定数や化学反応の進行といった内容も、熱力学を使って考えることができることがわかった。
| ↑1 | この系における1モルあたりの内部エネルギー、エントロピーを U, S とする。 |
|---|---|
| ↑2 | 状態方程式PV=nRTより。 |
| ↑3 | 系の大きさをa倍すると、状態変数の大きさもa倍されるような性質を示量性と呼ぶ。7.1ギブズエネルギーにも記載したように物質量n, 体積V, 内部エネルギーU, エントロピーS, エンタルピーH, ギブズエネルギーG, ヘルムホルツエネルギーA は示量性を持つ。一方、圧力Pや温度Tにはこのような性質はない。 |
| ↑4 | 今回の話は2成分とも気体で反応が起きることを想定している。いす形←→船形のシクロヘキサンの2つの立体配座間の構造変化を想像すると良いかもしれない。ノルマルブタン(CH3CH2CH2CH3)とイソブタン(CH3CH(CH3)2)の異性化も反応物と生成物による化学反応式としてはこのように書くことができるだろう。 |