圧縮因子とビリアル状態方程式
実在気体では凝縮が起きる以外にも、気体の状態方程式の形も理想気体の PV=nRT の形から変わってくる。そこで、圧縮因子として
という値を使って、理想気体からのずれを表すことがある。
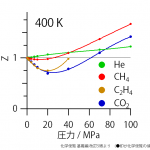
400Kにおけるいくつかの物質の圧縮因子*1化学便覧 基礎編 改訂5版 記載のデータをプロットしたもの。●印が化学便覧記載のデータ。データ間は曲線でつないだ。
理想気体の場合、この値は常に1である。一方、実在気体では上のグラフのように、圧力が高いとZの値は大きくなり、圧縮しにくくなる。また圧力が低いと、引力の関係で1よりも小さくなることがわかる。つまり、圧縮因子は圧力や体積によって変化する。このような圧縮因子の変化を記述するための方法として、圧縮因子をモル体積![]() の逆数、
の逆数、![]() を使って
を使って
のように展開(ビリアル展開)することがある。
このときのB, C,…といった係数は第2ビリアル係数、第3ビリアル係数と呼ばれ、状態方程式の形で書いた
という式はビリアル状態方程式と呼ばれる。
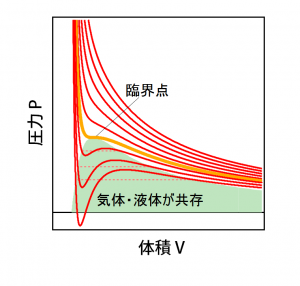
ファンデルワールス式と等温線
物理学で、簡素な理論による近似式と実測値が合わないとき、簡素な近似式をより実測を反映した式にするための修正方法にはいくつかある。1つはビリアル展開のように、もともと1次式だったものに2次、3次といった項を追加して、とにかく式が実測に近づくような多項式にしてしまうようなやり方である。もう1つの方法は、理論式に物理的に適切なパラメータを追加して、式を実測に近づけるようにする方法である。このようなアプローチをとる実在気体の状態方程式の1つとして、ファンデルワールス式と呼ばれる
のような式が知られている。ここで出てきた a, b は気体によって異なる値を持つ定数である。ファンデルワールス式では、圧力低下における引力の影響や、体積が小さくなった時の分子の大きさの影響を状態方程式に取りいれるために、理想気体の状態方程式の圧力、体積の部分に体積、物質量の影響を明示的に取り入れた式になっている。この式は19世紀に提唱された近似式であるが、凝縮の影響についてもある程度取り入れることに成功している点でも興味深い式である。
実際にファンデルワールス式を使って描いた体積と圧力の関係(等温線)が上のグラフ(実線)である。温度が高いときは、理想気体の等温線(P=nRT/V:反比例のグラフ)と比較的近い形になっているが、温度が低下するに従って理想気体とは違った形になっていく。二酸化炭素の場合なら、304 K において等温線(橙色)は臨界点を通り、これより下の温度では極大と極小点が出現するようになる。実際の等温線では臨界温度よりも低い温度では凝縮により圧力一定の状態が現れるので、ファンデルワールス式は凝縮の等温線までは再現できない。ただ、ファンデルワールス式による等温線をある圧力で分割して2つの閉曲線を作って極大点を含む領域(下図adbで囲まれた領域)と極小点(下図becで囲まれた領域)を含む領域の面積が同じになるようにすると、実際の等温線に対応させることができるという性質も持っている。
 「Wikipedia: Van der Waals equation」より
「Wikipedia: Van der Waals equation」より
ファンデルワールス定数と臨界点
ファンデルワールス式を展開して変形すると、モル体積についての3次方程式、$$PV-Pnb+\frac{n^2}{V}a-\frac{n^3}{V^2}ab=nRT $$ $$ \rightarrow \overline{V}^3-\overline{V}^2b+\frac{a\overline{V}}{P}-\frac{ab}{P}=\frac{RT\overline{V}^2}{P} $$ $$ \rightarrow \overline{V}^3-\left(b+\frac{RT}{P}\right)\overline{V}^2+\frac{a}{P}\overline{V}-\frac{ab}{P}=0 \tag{4.2.5}$$にできる*2n=1のときの体積がモル体積![]() であり、両辺に
であり、両辺に![]() を掛けてまとめた。 なお臨界温度以下ではこの3次方程式は3つの実数解を持ち、臨界温度以上では1つの実数解しか持たない。そこでこの三次関数は臨界点において3重解を持つ形、$$\left(\overline{V}-\overline{V}_c\right)^3=0 $$ $$ \rightarrow \overline{V}^3-3\overline{V}_c\overline{V}^2+3\overline{V}_c^2\overline{V}-\overline{V}_c^3=0 \tag{4.2.6}$$となっていると考え、元のファンデルワールス式と比較すると、$$b+\frac{RT_c}{P_c}=3\overline{V}_c, \frac{a}{P_c}=3\overline{V}_c^2, \frac{ab}{P_c}=\overline{V}_c^3 \tag{4.2.7}$$となるので、結局ファンデルワールス式の2つのパラメータ a, b と臨界温度
を掛けてまとめた。 なお臨界温度以下ではこの3次方程式は3つの実数解を持ち、臨界温度以上では1つの実数解しか持たない。そこでこの三次関数は臨界点において3重解を持つ形、$$\left(\overline{V}-\overline{V}_c\right)^3=0 $$ $$ \rightarrow \overline{V}^3-3\overline{V}_c\overline{V}^2+3\overline{V}_c^2\overline{V}-\overline{V}_c^3=0 \tag{4.2.6}$$となっていると考え、元のファンデルワールス式と比較すると、$$b+\frac{RT_c}{P_c}=3\overline{V}_c, \frac{a}{P_c}=3\overline{V}_c^2, \frac{ab}{P_c}=\overline{V}_c^3 \tag{4.2.7}$$となるので、結局ファンデルワールス式の2つのパラメータ a, b と臨界温度![]() 、臨界圧力
、臨界圧力![]() 、臨界モル体積
、臨界モル体積![]() の関係は
の関係は
となる。実際、 a, b は臨界点の測定値から求められたものが使用されている。
このように、ファンデルワールス式による等温線は、臨界点の温度、圧力、モル体積から得られた2つの係数のみを使って表しているにもかかわらず、凝縮領域まで含めた等温線を描くことができるのは大変興味深い。