根平均二乗速度
前節の分子あたりのエネルギーの式(3.4.8)から分子の平均速度を出すことができる。Etrans は分子の運動エネルギーだったので、$$E_{trans}=\frac12 m\overline{v^2}=\frac32 k_B T$$ $$\rightarrow \overline{v^2}=\frac{3k_B T}{m} \tag{3.5.1}$$ のように変形することができるだろう。
さらに、この量![]() の平方根をとると、平均的な分子の速さが計算できることが分かるだろう。この値
の平方根をとると、平均的な分子の速さが計算できることが分かるだろう。この値
は根平均二乗速度と呼ばれる。また、同じ温度でも、分子が重いと速度が遅いということもわかるだろう。なお、![]() は速度の二乗の平均値である。速度
は速度の二乗の平均値である。速度![]() の平均とは異なることに注意したい。*1速度 v には符号があるので +v に動く分子と -v に動く分子があって、平均すると0になることがあるが、その場合も v を2乗して平均した値は同じ0にはならない。
の平均とは異なることに注意したい。*1速度 v には符号があるので +v に動く分子と -v に動く分子があって、平均すると0になることがあるが、その場合も v を2乗して平均した値は同じ0にはならない。
1次元並進運動の速度分布関数
それでは1個1個の分子の速度はどうなっているだろうか。ここまでの結果では平均的な速さは計算されたが、1個1個の分子の速さがどのような分布を取っているかはわからない。このような速度の分布は速度分布関数と呼ばれる。ある方向について、分子の速度分布がどのようになっているかを示す式は、
となる。これは1次元並進運動の速度分布関数(1次元のマクスウェルの速度分布関数)と呼ばれる。速度なので符号があり、0を中心にしたガウス分布になっているということは、平均は0であるが、y, z 方向の速度成分もあるので分子が静止しているわけではない。1次元並進運動の速度分布関数を使うと、N 個の分子のうち x 軸方向について ![]() から
から ![]() の範囲の速度で運動する分子の割合を、$$\frac{dN}{N}=f(v_x)dv_x \tag{3.5.4}$$のように書くことができる。
の範囲の速度で運動する分子の割合を、$$\frac{dN}{N}=f(v_x)dv_x \tag{3.5.4}$$のように書くことができる。

上図は窒素分子の場合の各温度での1次元並進運動の速度分布関数 ![]() である。
である。
マクスウェルの速さ分布関数
速度ではなくその大きさ(速さ)のみを取り扱った場合、その平均は0ではない。また、その分布についても速度分布関数とは異なるものになる。3次元空間で速さについての分布関数を出すには、![]() がある値
がある値![]() になる組合せで確率を求めればよくて*2速度空間の体積素片
になる組合せで確率を求めればよくて*2速度空間の体積素片 ![]() を球面で積分して出せる。詳細は現代物理化学p215あたりをどうぞ。、その結果は
を球面で積分して出せる。詳細は現代物理化学p215あたりをどうぞ。、その結果は
となる。この式は、マクスウェルの速さ分布関数(マクスウェル分布,マクスウェル-ボルツマン分布*3「ボルツマン分布」とは異なる。)と呼ばれる式で、分子がある速さになっている確率を示す式である。式としては対数関数と2次関数の掛け算なので、ある速さ![]() まで増大した後、指数関数的に減少して0に近づいている。ここでピークの速さ
まで増大した後、指数関数的に減少して0に近づいている。ここでピークの速さ![]() は確率分布の最頻値であり、最大確率の速さと呼ばれている。
は確率分布の最頻値であり、最大確率の速さと呼ばれている。
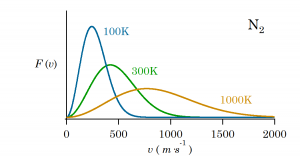
上図は窒素分子の場合の各温度での ![]() をプロットしたものとなる。
をプロットしたものとなる。
エネルギーの分布関数
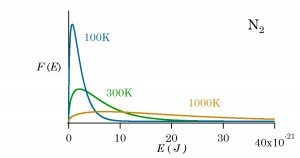
エネルギーについてもその頻度の分布関数があり、
のようになる。これは先の速度分布の式の![]() 部分を。2E/m で置き換え微分係数を dv から dE に置き換える操作をすることで出てくる*4
部分を。2E/m で置き換え微分係数を dv から dE に置き換える操作をすることで出てくる*4![]() のように速度分布関数を置き換える。。これまで同様、分子のエネルギーがある値をとる確率を表す式である。
のように速度分布関数を置き換える。。これまで同様、分子のエネルギーがある値をとる確率を表す式である。