原子の内部構造や原子スペクトルを説明するにあたって当時の人たちは、光や物質は全て粒子としての性質を持つだけでなく、波としての性質も併せ持っているという考え方を導入することにした。光についてはそれまでも、波か粒子か長らく議論の的になってきた。ホイヘンスが光の波動説を唱え、ニュートンが光の粒子説を提唱したのは17世紀のことである…が、物質が波と考えられることはそれまでなかった。ところが物質を波として考えることにすると、それまで説明が難しかった原子スペクトルもうまく説明できるようになるのである。

波としての光と粒子としての光

はじめに、光について波と粒子の性質について考えてみることにする。光が波と粒子の両方の性質を持つことが明らかになったのもまた20世紀に入ってからだ。波としての光は電磁波として知られているもので、たとえば x 方向に進む光は時間 t と位置 x に依存する電場の関数として
$$E(t,x)=E_0\sin\left(2\pi\left(\frac x\lambda-\nu t\right)\right)\tag{1.2.1}$$

と表すことができる。ここでλは波長、νは振動数、E₀は波の振幅を意味しており、光の速度 c を使って λ=c/ν の関係がある。この波としての光の性質は光の干渉や回折の性質から19世紀頃既に確認されていたものだ。また、光を波として表した場合、光の色は波長（または振動数）が対応し、光の強さ(エネルギー)は振幅の二乗 E² が対応している^*1つまり光を波として考えた時、振動数(波長)と光のエネルギーには関係がない。。

さらに今日では、光は波としての性質を持つだけではなく、エネルギー hν, 運動量 hν/cを持った光子という粒子でもあると考える。h はプランク定数と呼ばれる数で、6.6×10^-34 m²kg/s という非常に小さな値だ。このような光子が n 個あったとすると、光の強さは光子のエネルギー hν を光子の数 n と掛け合わせたもの、つまり nhν であると考えることになる。ここで重要なのは光子のエネルギーに振動数 ν が掛かっていることで、光を波として考えた時、振動数はエネルギーには関係していなかったものが、エネルギー hν の光子を考えることで、光のエネルギーは振動数にも比例するものになる。

光の性質を説明するにあたって、波と粒子という、全く異なる２つの性質をなぜわざわざ導入することになったか。それはそう考えないと説明できない現象が当時多数発見されていたからだ。たとえば光電効果という現象がある。光電効果は物質に光を当てると電子が飛び出してくる現象である。光電効果には、

• 照射する光の振動数が低いとどんなに強い光を当てても起きず、ある一定以上の振動数の光が必要。
• 照射する光の振動数を大きくすると、飛び出してくる電子1個あたりのエネルギーは大きくなる一方、飛び出してくる電子の数には変化がない。
• 照射する光を強くすると、飛び出してくる電子1個あたりのエネルギーは変わらない一方、飛び出してくる電子の数が増える。

といった性質がある。

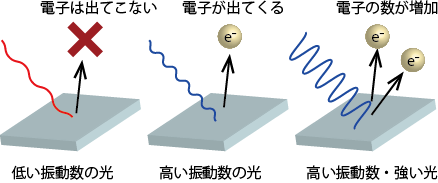
要するに、赤い光をどんなに強く当てても電子が出てこないのに、青い光だとものすごく弱くても電子が出てくるといったことが起きる。ところが波としての光だけで考えると、光のエネルギーに波長や振動数は影響せず、振幅 E₀ だけで決まるので、色(振動数)によって電子が出てきたり出てこなかったりする現象を説明できない。

一方、粒子の性質を持つ光を考えると、色（振動数）は光子1個のエネルギーにも対応しているので、原子内から電子が飛び出してくるには最低限必要なエネルギーがあると考えることができるようになる。つまり、青い光だと最低限のエネルギー以上だから光電効果が起きるけれども、赤い光では最低限のエネルギーよりも小さいので電子が飛び出してこない…と説明ができる。さらに、光を強くすると電子の数が増えるのも物質に照射される光子の数が増えるから、と考えるだけで説明がつくことになる^*2アインシュタインがノーベル賞を受賞したときの受賞理由はこの現象（光電効果）の説明である。

物質の場合：物質波

それでは物質を波として、粒子として考えるというのは、どのようなことだろうか？ 粒子として、波としてのエネルギー、運動量を紹介しよう。
まず、粒子として物質は簡単で、たとえば質量 m, 速度 v の物質について考えるとすると、ニュートンの力学どおり、$$エネルギーE=\frac{1}{2}mv^2,\quad 運動量 p=mv\tag{1.2.2}$$の粒子を考えればよい。
一方、波としての物質を考えるときは、まず物質がある振動数νの波であると考え、そのエネルギーと運動量が光のときと同様、$$エネルギーE=h\nu,\quad 運動量 p=h\nu/c\tag{1.2.3}$$と表せると考える。
つぎに、アインシュタインの特殊相対論から出てくるエネルギーと質量・光速の関係の式 E=mc² と組み合わせて$$E=mc^2, E=h\nu \quad\rightarrow\quad mc^2=h\nu\tag{1.2.4}$$として、光速 c で割ることで$$mc=\frac{h\nu}{c}=\frac{h}{\lambda}\tag{1.2.5}$$が得られる。ここで hν/c は運動量だったので、物質の運動量 p=mv を対応付けることで

が得られる。これが波としての物質（物質波）の波長を示す式である。

実際に計算してみると、たとえば1 gの物体（１円玉）が1 km/sで直進しているとその波長は6.6×10^-34 mとなり、小さすぎて観測が不可能な長さとなる。
一方、物質が電子だと質量：9×10^-31 kg なので、仮に電子が 1000 km/s で運動しているとその波長は 7×10^-10 m = 0.7 nm となって固体中の原子間隔くらいになる。実際に物質に電子をぶつけると波としての回折現象が観測され、電子の波動性の実証例となっている。
これを応用したのが電子顕微鏡で、電子をナノメートル以下の波長の波として考えることで、通常の可視光線（波長数百ナノメートル）では見ることができない大きさのものを見ることを実現している。