はじめに
このページは千葉大学で工学部の1年生向けに行っている一般化学の講義、”化学基礎A”の野本担当分の講義内容/テキスト/資料と復習用補足説明をまとめたものです。
千葉大学の化学基礎/基礎化学は物質の構造、状態、変化といった物理化学の領域を扱う化学基礎Aと、有機物質の結合、構造、反応といった有機化学領域を扱う化学基礎Bに分かれており、本講義は化学基礎Aですので、このページでは物理化学の基礎となる内容をまとめてあります。有機化学や無機化学が個々の物質についての性質や反応、合成方法等を取り扱うのに対して、物理化学では物理学的な考え方を元に、物質の構造や状態、変化について物質全般に通用する原理や仕組みについて取り扱います。
物理的な視点で物質の状態や変化を考えるといっても、原子や分子を1つ1つ微視的(ミクロ)に見たときと、原子や分子を集団的(マクロ)として見たときでは、同じ現象でも扱い方が違ってきます。たとえば、水素と酸素が反応して水になる反応について考えるとき、酸素や水素分子、水分子の構造や、個々の酸素と水素分子の化学結合がどのように切れて反応するかといった反応機構はミクロな性質といえるでしょう。一方、この反応は酸素、水素の圧力や混合割合によっても全体の反応の進み方が違ってきますが、こうした内容は集団としての物質のマクロな挙動を考えないといけないでしょう。
どちらも元は分子でできているのだから、ミクロな性質からマクロな挙動も分かるはずだと思われるかもしれません。確かに、分子や原子1個1個の運動方程式を考えて、その運動を追跡すればマクロな性質もわからないでもありません。ただ、困ったことに、我々が知りたい分子や原子の数はコップ一杯の水でさえ1024個以上あり、1個1個の分子の運動を追跡するには数が多すぎます。*1仮にコンピューター上の12バイトで1個の分子の位置をあらわせるとして、1 TB=1012バイトのハードディスクで表せる分子の数は8×1010個しかありません。地球上のハードディスクを全て合わせても、ある時間のコップ一杯の分子の位置を記録できるかできないか…といったところでしょうか。
それに、分子や原子が仮想のものではなく、実際に存在する粒子であることが確認されたのは100年ほど前のことなのです。歴史的に物理学では物質のマクロな性質とミクロな性質で別々に理論が作られ、使われてきました。現在でも原子や分子の構造や化学結合といった微視的な情報を知りたい場合は量子力学を、気体の圧力のような巨視的性質について知りたい場合は熱力学が使われ、それぞれ重要な役割を果たしています。そこで、この講義では量子力学の基礎から分子・原子の構造についての話と熱力学の基礎から化学平衡についての内容を扱うことにしています。
数学的準備
大学で出てくる数式には高校では習ったことのない数学や、見慣れた形式と違った形式の数式が出てくることも多く、そこで躓いてしまうことがよくあります。この講義で出てくる数式で、高校では出てこないものや、見慣れないかもしれない書き方をここでとりあえず取り上げておきます。
対数の書き方
lnって何ですか?…という質問がありました。
対数は一般にはb=logaNと底を明示して表記するわけですが、底が10の常用対数、底がeの自然対数では底が省略されることが頻繁にあります。
単純にlogxと表記されているときは分野、文脈によって常用対数だったり自然対数だったり、場合によりけりで底が変わりますが、lnxと表記されているときの底はほぼ間違いなく自然対数を意味します。つまり、
b = ln x は b = loge x 、 すなわち x = eb を満たすb の値です。
オイラーの公式
eiθ と sinθ, cosθ には自然対数の底 e と虚数単位 i を使った以下の関係があり、オイラーの公式として知られています。
$$e^{i\theta}=\cos\theta+i\sin\theta\tag{0.1.1}$$ また、この式から$$e^{i\pi}=\cos\pi+i\sin\pi=-1\tag{0.1.2}$$ということもわかるでしょう。
偏微分
偏微分とは、複数の変数が入った関数において、1つの変数以外の変数は定数と考えて行う微分のことです。関数f(x)の微分が![]() と表記されるのに対し、偏微分は
と表記されるのに対し、偏微分は![]() と表記されます。
と表記されます。
たとえば、多変数関数$$f\left(x,y,z\right)=x^3+yzx^2+y^2+z^2+zx+yz$$があったとして、x について偏微分を行たい場合、まずはこれを
$$f\left(x,y,z\right)=x^3+(yz)x^2+(z)x+(y^2+yz+z^2)$$と考え、x以外の変数、つまり yz、 z、 y2+yz+z2 を定数と考えて微分を行います。その結果出てくる
$$\frac{\partial f(x,y,z)}{\partial x}=3x^2+(yz)2x^1+z$$がf(x,y,z)のxについての偏微分です。
偏微分が意味するもの
1変数の関数についてのグラフy=f(x)があったとき、その導関数![]() はある座標xにおける接線の傾きを意味していました。
はある座標xにおける接線の傾きを意味していました。
関数が2変数になった場合の偏微分も同様に傾きと考えて理解することができます。まずは2変数の関数をz=g(x,y)があったとして、この関数を3次元にプロットすると曲面になります。このとき、xについての偏微分![]() はこの曲面をあるy座標で切断した時の切断面(xz平面)上の曲線のx方向の接線の傾きになります。同様にyについての偏微分
はこの曲面をあるy座標で切断した時の切断面(xz平面)上の曲線のx方向の接線の傾きになります。同様にyについての偏微分![]() なら、この曲面のあるx 座標で切断したときのyz 平面上の曲線のy方向の接線の傾きです。
なら、この曲面のあるx 座標で切断したときのyz 平面上の曲線のy方向の接線の傾きです。
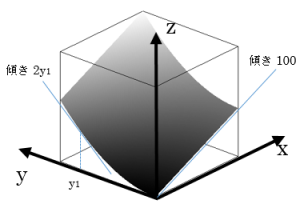 たとえば、右の曲面はf(x,y)=100x+y2 について、f(x,y)の値をz方向にプロットしたものです。これをxについて偏微分した結果$$\frac{\partial f}{\partial x}=100$$は、この曲面のx方向の傾きです。一方、yについて偏微分した結果$$\frac{\partial f}{\partial y}=2y$$は、yの各座標値におけるy方向の接線の傾きを表しています。
たとえば、右の曲面はf(x,y)=100x+y2 について、f(x,y)の値をz方向にプロットしたものです。これをxについて偏微分した結果$$\frac{\partial f}{\partial x}=100$$は、この曲面のx方向の傾きです。一方、yについて偏微分した結果$$\frac{\partial f}{\partial y}=2y$$は、yの各座標値におけるy方向の接線の傾きを表しています。
参考書など
この講義のための講義ノートをまとめるにあたって、以下の教科書を参考にしました。
現代物理化学
寺嶋 正秀・馬場 正昭・松本 吉泰 著 化学同人 2015年 ISBN-13: 978-4759818093
現在販売されている物理化学の教科書で一番のお勧め?…というか気に入っています。著者が日本人なので高校からの接続が良く、内容が冗長すぎることもなく、カラーで綺麗です。分子分光学的な内容など物理化学の研究の基礎知識になりそうな内容は大体入っている感じ。ギブズエネルギーの説明などはすっきりわかりやすいと思います。
新物理化学
坪村 宏 著 化学同人 1994年 ISBN: 978-4759802672
この講義のためにかなり参考にしましたが、残念ながら既に絶版になっています。特に量子論から構造化学の項目はわかりやすくお勧めで、量子力学の仮説のあたりの説明はこちらの本の書き方を踏襲しています。
物理化学(基礎から理解する化学1)
久下謙一・森山広思・一國伸之・島津省吾・北村彰英 著 みみずく舎 2008年 ISBN:978-4-87211-904-6
講義を前任の先生から引き継いだ際、別の先生が行う同時間帯の講義ともどもこちらの本が教科書になっていたため、講義内容・順番はこの本を参考にしました。他の本と比べると安価ですが、わかりやすいかといわれると、どうでしょうか…。
アトキンス物理化学
昔から物理化学の教科書として定番の本です。
マッカーリサイモン物理化学
こちらも近年、物理化学の教科書として定番の本です。
量子化学
原田義也著
水素原子の波動関数、量子力学の仮説など参考にしました。なお、現在は改訂版が出ています。
※千葉大学からは2020/09/04まで電子版が無料で読めるようです。⇒量子化学 改訂版 上巻 (アクセス方法)
量子力学Ⅰ
小出昭一郎 著
シュレディンガー方程式の導入、量子力学の仮説など参考にしました。
趣味で量子力学
広江 克彦 著 理工図書 2015年 ISBN: 978-4844608370
量子力学について独習するには良い本だと思います。
この本の著者の方が作られているEMANの物理学というサイトもいろいろ勉強になります。
印刷版について
印刷された冊子版が欲しいという方のためにA4冊子版を作りました。Amazonにて入手可能ですのでご利用ください。若干の加筆修正はあるものの内容はWeb版とほぼ同じです。
『化学基礎講義ノート「物理化学ことはじめ」』 ISBN:978-4-8020-8037-8
| ↑1 | 仮にコンピューター上の12バイトで1個の分子の位置をあらわせるとして、1 TB=1012バイトのハードディスクで表せる分子の数は8×1010個しかありません。地球上のハードディスクを全て合わせても、ある時間のコップ一杯の分子の位置を記録できるかできないか…といったところでしょうか。 |
|---|

