理想気体の状態方程式や分圧の法則などを考えるにあたって、その理論的裏付けとして発展してきたのが気体分子運動論である。この節では分子の運動をモデル化して、温度や圧力が何に対応しているかを考えてみることにする。
前提条件
ここで考える気体分子については、以下のような前提条件をもとに気体中の分子の運動をモデル化して気体の振る舞いを説明することにする。
- 気体分子は内部構造を持たない
- 気体分子は質量を持つが大きさは無視できるほど小さい
- 気体分子の運動はランダムであり、分子間相互作用はない
- 分子間の衝突・壁との衝突は弾性的(衝突によって運動エネルギーを失わない)
圧力:分子が壁に及ぼす力として計算
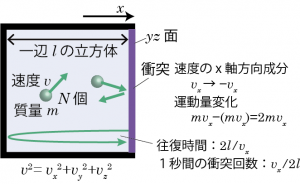
このような前提の元、分子を一辺 l の立方体の箱に入れて圧力について考えてみよう。
まずは1個の分子を箱に入れ、分子の x 方向の速度成分が vx であるして x 方向のみを考えるなら、分子が壁に衝突してから次に同じ壁に衝突するまでの時間は ![]() になる。…ということは、Δt 秒間に分子が壁に衝突する回数は
になる。…ということは、Δt 秒間に分子が壁に衝突する回数は ![]() になるだろう。
になるだろう。
ここで、分子が衝突した時の運動量変化を考えると、もともと 速度 ![]() で進んでいた分子が衝突後は
で進んでいた分子が衝突後は ![]() になることになるので、運動量変化は
になることになるので、運動量変化は ![]() となる。Δt 秒間に衝突した分子の数、
となる。Δt 秒間に衝突した分子の数、 ![]() を掛け合わせた
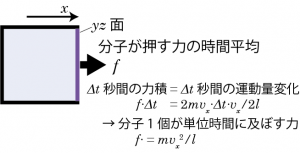
を掛け合わせた ![]() は、Δt 秒間の分子の運動量変化の合計である。一方、分子が何回も衝突することによって、壁には平均的に f の力を受けていると考えるとすれば、Δt 秒間に分子衝突によって壁が受ける力積は fΔt となる。従って運動量変化=力積の関係、$$2Nmv_x \Delta t\frac{v_x}{2l} = f\Delta t \tag{3.4.1}$$ から、単位時間あたりに分子1個が壁に及ぼす力は$$f=\frac{mv_x^2}{l} \tag{3.4.2}$$となる。
は、Δt 秒間の分子の運動量変化の合計である。一方、分子が何回も衝突することによって、壁には平均的に f の力を受けていると考えるとすれば、Δt 秒間に分子衝突によって壁が受ける力積は fΔt となる。従って運動量変化=力積の関係、$$2Nmv_x \Delta t\frac{v_x}{2l} = f\Delta t \tag{3.4.1}$$ から、単位時間あたりに分子1個が壁に及ぼす力は$$f=\frac{mv_x^2}{l} \tag{3.4.2}$$となる。
箱の中に分子 N 個の分子が入っている場合、1個の分子が平均的に壁に及ぼす力が1秒あたり f ならば、N 個の分子なら f N だけ力を及ぼしていることになる。これは圧力に直すと ![]() となる。先ほど求めた
となる。先ほど求めた ![]() を代入すると、$$P=\frac{Nmv_x^2}{V} \tag{3.4.3}$$ となる…と、ここまでは壁の1方向のみを考えてきたが、実際には分子が飛んでいる方向は同じではない。ただ、箱が等方的で x, y, z どちらの方向でも平均的な速度が同じようなものであるとすると、実際の分子の速度を
を代入すると、$$P=\frac{Nmv_x^2}{V} \tag{3.4.3}$$ となる…と、ここまでは壁の1方向のみを考えてきたが、実際には分子が飛んでいる方向は同じではない。ただ、箱が等方的で x, y, z どちらの方向でも平均的な速度が同じようなものであるとすると、実際の分子の速度を ![]() として、速度の2乗の平均については$$\overline{v^2}=\overline{v_x^2}+\overline{v_y^2}+\overline{v_z^2} \tag{3.4.4}$$ と考えることができる*1
として、速度の2乗の平均については$$\overline{v^2}=\overline{v_x^2}+\overline{v_y^2}+\overline{v_z^2} \tag{3.4.4}$$ と考えることができる*1![]() など上線付は平均を表すことにする。。ここから
など上線付は平均を表すことにする。。ここから
という式を出せる。つまり、気体の圧力というのは分子の質量と速度によって決まるものであるということになる。
温度と分子運動:気体分子の平均的な運動エネルギーは温度で決まる。
次に、この式を理想気体の状態方程式、 ![]() の式と比較してみよう。2つの式を比較するため、状態方程式の物質量をアボガドロ数 NA を使って、
の式と比較してみよう。2つの式を比較するため、状態方程式の物質量をアボガドロ数 NA を使って、![]() と書くなら、$$PV=\frac{N}{N_A}RT \tag{3.4.6}$$である。また、
と書くなら、$$PV=\frac{N}{N_A}RT \tag{3.4.6}$$である。また、![]() の部分を1分子あたりの運動エネルギー
の部分を1分子あたりの運動エネルギー ![]() を使って書き換えて変形すると、$$PV=\frac23 N\left(\frac12 m\overline{v^2}\right) \rightarrow PV=\frac23 N E_{trans} \tag{3.4.7}$$となり、2つの式を比較すれば Etrans は比例係数 kB を使って
を使って書き換えて変形すると、$$PV=\frac23 N\left(\frac12 m\overline{v^2}\right) \rightarrow PV=\frac23 N E_{trans} \tag{3.4.7}$$となり、2つの式を比較すれば Etrans は比例係数 kB を使って
と書けることもわかる。つまり、気体中の分子の運動エネルギーは温度に比例する、逆に言えば気体の温度というのは分子の運動エネルギーに対応していることを意味する。ここで出てきた比例定数 kB はボルツマン定数と呼ばれる定数であり![]() である。
である。
分子1個あたりの持つ運動エネルギーが ![]() ということは、分子集団が持つエネルギーなら分子の個数を掛けた運動エネルギーを持つことになる。気体が持つ全てのエネルギーの和は内部エネルギーと呼ばれる。本節では、分子の内部構造を考えないような単原子分子理想気体について議論しているので、気体が持つエネルギーは運動エネルギーのみである。ということは、n モルの分子の内部エネルギーは
ということは、分子集団が持つエネルギーなら分子の個数を掛けた運動エネルギーを持つことになる。気体が持つ全てのエネルギーの和は内部エネルギーと呼ばれる。本節では、分子の内部構造を考えないような単原子分子理想気体について議論しているので、気体が持つエネルギーは運動エネルギーのみである。ということは、n モルの分子の内部エネルギーは
となる。
エネルギー等分配の法則
ところで、エネルギー等分配の法則というものがある。
3次元空間の分子の運動はx,y,zの3方向が取りうる自由度であり、通常これらの方向に区別はない。こういった場合、先に出てきたエネルギー![]() を3つの方向に分けて、1方向あたり $$E=\frac12 k_B T \tag{3.4.10}$$のエネルギーを持っていると考えることができるだろう。
を3つの方向に分けて、1方向あたり $$E=\frac12 k_B T \tag{3.4.10}$$のエネルギーを持っていると考えることができるだろう。
外部からエネルギーが加えられたときも各方向同じようにエネルギーが分配され、各方向等しく ![]() というエネルギーを持つことになる(エネルギーが加わった後の温度を T’ とする)。このように、分子の運動の自由度に対してエネルギーを等しく分けることができるという考え方はエネルギー等分配の法則と呼ばれる。
というエネルギーを持つことになる(エネルギーが加わった後の温度を T’ とする)。このように、分子の運動の自由度に対してエネルギーを等しく分けることができるという考え方はエネルギー等分配の法則と呼ばれる。
この章では単原子分子理想気体を扱っているため並進運動のエネルギーのみに等分配しているが、2原子分子になった時などは分子内の運動(回転や振動)にもエネルギーを分配する必要が出てきてさらに重要になってくる。
| ↑1 |
|---|