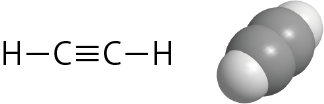アセチレン
ここからは、より複雑な分子についての軌道を考えていく。
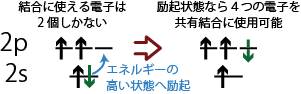
アセチレン(上図)は炭素原子はCC三重結合とCH単結合を持つが、炭素原子の原子軌道に下から順番に電子を詰めていくと、最外殻の2p軌道には2個の電子があるだけなので、これら2個の電子による結合だけではアセチレン分子をつくることができないことが分かるだろう。
一方、2s軌道にいた2個の電子のうち1個が2p軌道に移った状態(励起状態、エネルギーが少し高い状態)を考えたならば、新たに電子が入った2p軌道と、電子が1個減った2s軌道も結合に関与することができるようになる。
このように考えたとき、2つの2p軌道(2px,2py)はπ結合を生成するのは明らかだろう。
それではH-C-C-Hの軸方向(z方向)についてはどうだろうか? 隣の炭素や水素と結合するのは2s軌道だろうか?2pz軌道だろうか?
実のところ、2s軌道の電子と2pz軌道の電子の核からの平均距離は近いこともあり、隣の原子の軌道は2s軌道、2pz軌道の両方と軌道の重なりを持つことができる。
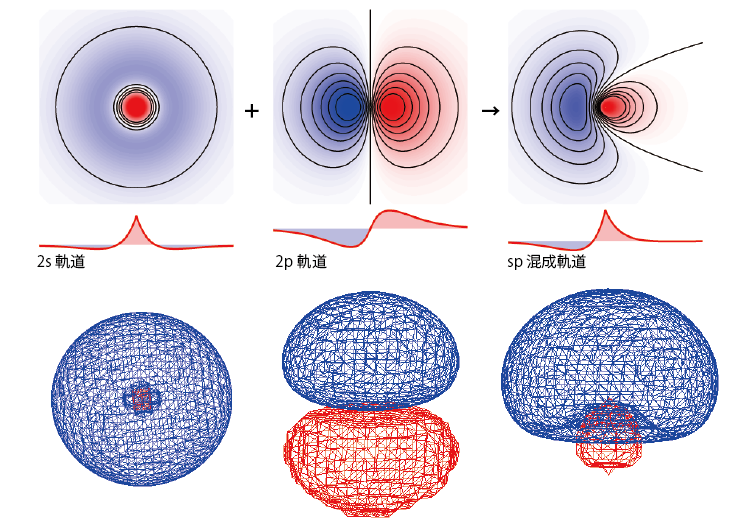
このような状況をうまく説明できるものとして混成軌道というものがある*1本来、混成軌道は原子価結合法と呼ばれる方法で分子の波動関数を表すために導入されたものであるが、ここでは複数の原子軌道の寄与がある化学結合の電子の重なりを分離して説明するために導入した。一般的な物理化学・量子化学の授業で原子価結合法に基づいて混成軌道が導入されるときは式の形は同じでも考え方がいろいろ違うので注意してください。。隣の原子と結合を作るときに2s軌道、2pz軌道の両方と軌道の重なりを持つことを考慮して、まずは2s, 2pzの2つの軌道のかわりにこれらを足し引きした$$\phi_1=\frac1{\sqrt 2}\left(\phi_{2s}+\phi_{2pz}\right)$$ $$\phi_2=\frac1{\sqrt 2}\left(\phi_{2s}-\phi_{2pz}\right)$$ という2つの波動関数に電子が1個ずつ入っていると考えることにする。こうしてできた2つの軌道は元の2s, 2pz軌道と違い、z方向の向き以外は電子の存在確率が2つの軌道で同じになる。
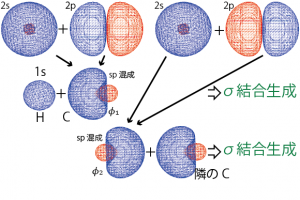
そこで、これら2つの軌道の各々が、隣の水素、炭素原子の軌道と重なり合い、電子を2個ずつ共有することで結合が生成している*2C-Hの結合なら、1個の電子が入った水素の1s軌道と、やはり1個の電子が入った上記![]() 軌道が結合性軌道、反結合性軌道を形成し、2個の電子が結合性軌道に入って結合を生成することでより安定な状態になる。…と考える。こうすれば2sか2pのどちらか?…といったことも考えず両方の軌道の寄与を考えることができる。ここで出てきた2つの波動関数
軌道が結合性軌道、反結合性軌道を形成し、2個の電子が結合性軌道に入って結合を生成することでより安定な状態になる。…と考える。こうすれば2sか2pのどちらか?…といったことも考えず両方の軌道の寄与を考えることができる。ここで出てきた2つの波動関数![]() がsp混成軌道と呼ばれるものである。
がsp混成軌道と呼ばれるものである。
このように、励起状態を考慮して作った新たな軌道で結合性軌道を作ったほうが、もとの原子軌道に電子をエネルギーの低い順に詰めていった状態に比べてエネルギーよりも低くなるために、炭素原子では混成軌道による化学結合が形成されることになる。
アセチレンの場合2sと2p軌道各1個をsp混成軌道(![]() )に組み替えた。混成を行わなかった残りの2p軌道についてはそのままπ結合を生成すると考える(
)に組み替えた。混成を行わなかった残りの2p軌道についてはそのままπ結合を生成すると考える(![]() )。このような
)。このような![]() の4つの軌道に1個ずつ電子が入っている状態を考え、隣の原子の軌道の重なりを作ることで、炭素原子は4つの結合を形成することになる。sp混成軌道によって作られる2つのσ結合(CーH,CーCの結合)と、残りの2つのp軌道によって作られる2つのπ軌道(両方が隣のCと結合)である。CC間で見た場合、1個のσ結合と2個のπ結合が生成することになり、三重結合と呼ばれることになる。
の4つの軌道に1個ずつ電子が入っている状態を考え、隣の原子の軌道の重なりを作ることで、炭素原子は4つの結合を形成することになる。sp混成軌道によって作られる2つのσ結合(CーH,CーCの結合)と、残りの2つのp軌道によって作られる2つのπ軌道(両方が隣のCと結合)である。CC間で見た場合、1個のσ結合と2個のπ結合が生成することになり、三重結合と呼ばれることになる。
これと同じように、原子軌道を足し算、引き算で組み合わせて作った混成軌道を使って結合性軌道、反結合性軌道が形成されると考えることで、アセチレンだけでなく、メタンの四面体構造、エチレンの平面構造などについても説明できるようになる。*3なお、上記混成軌道はやみくもに足し引きしてできたわけではない。もともとの各原子軌道は同じ軌道同士を積分すると1(電子の存在確率を全空間で足し合わせると1になる。例:![]() )、異なる軌道同士で積分すると0になる性質を持つ。(例:
)、異なる軌道同士で積分すると0になる性質を持つ。(例:![]() )。新たに作られた混成軌道においても、それぞれにおいて、上記関係が互いに満たされるよう、
)。新たに作られた混成軌道においても、それぞれにおいて、上記関係が互いに満たされるよう、![]() 、かつ
、かつ![]() にならないといけない。
にならないといけない。![]() という係数が掛かっているのもそのため(規格化のため)である。
という係数が掛かっているのもそのため(規格化のため)である。
エチレン
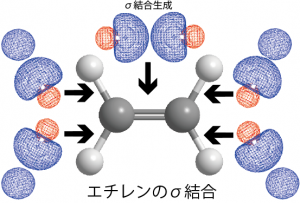
エチレンの場合は炭素原子に2つの水素と1つの炭素が結合して、全体として平面構造をとっている。
このような構造を説明できる混成軌道は2sと2つの2p軌道を使ったsp2混成軌道と呼ばれるものである。sp2混成軌道は次のように表され、混成でできた3つの軌道は同一平面上の3方向に向いている。
$$\phi_1=\frac1{\sqrt3}\phi_{2s}+\frac{\sqrt2}{\sqrt3}\phi_{2pz}$$ $$\phi_2=\frac1{\sqrt3}\phi_{2s}+\frac1{\sqrt2}\phi_{2px}-\frac1{\sqrt6}\phi_{2pz}$$ $$\phi_3=\frac1{\sqrt3}\phi_{2s}-\frac1{\sqrt2}\phi_{2px}-\frac1{\sqrt6}\phi_{2pz}$$ $$\phi_4=\phi_{2py}$$ 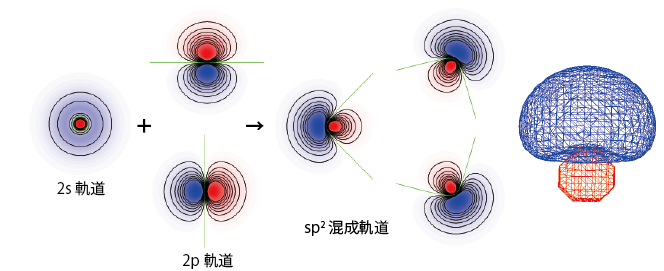
3方向を向いた![]() の3つの軌道には1個ずつ電子が入っているので、相手の原子の軌道と重なり、2個の電子を共有することでσ結合を生成することになる。
の3つの軌道には1個ずつ電子が入っているので、相手の原子の軌道と重なり、2個の電子を共有することでσ結合を生成することになる。
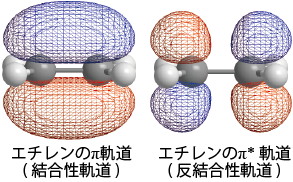
また、残された1個のp軌道(![]() )は隣の炭素原子のp軌道と重なり合ってπ軌道、π*軌道(下図)を形成するが、その際電子はπ軌道に入ってπ結合を生成する。この結果、エチレンのCC間はσ結合とπ結合の2個の結合が生成され、2重結合と呼ばれることになる。
)は隣の炭素原子のp軌道と重なり合ってπ軌道、π*軌道(下図)を形成するが、その際電子はπ軌道に入ってπ結合を生成する。この結果、エチレンのCC間はσ結合とπ結合の2個の結合が生成され、2重結合と呼ばれることになる。
メタン
メタンの場合は炭素原子に4つの水素がσ結合で結びついていて四面体構造を取っていることが知られている。このような状況を説明できる混成軌道は、2sと2px,2py,2pzすべてを使ったsp3混成軌道と呼ばれるもので、以下のように表される。$$\phi_1=\frac12\left(\phi_{2s}+\phi_{2px}+\phi_{2py}+\phi_{2pz}\right)$$ $$\phi_2=\frac12\left(\phi_{2s}+\phi_{2px}-\phi_{2py}-\phi_{2pz}\right)$$ $$\phi_3=\frac12\left(\phi_{2s}-\phi_{2px}+\phi_{2py}-\phi_{2pz}\right)$$ $$\phi_4=\frac12\left(\phi_{2s}-\phi_{2px}-\phi_{2py}+\phi_{2pz}\right)$$
これらの軌道を描いてみると、向きが異なるだけで電子存在確率が等しい4つの軌道が正四面体の中心から4つの頂点方向を向いている。これら4つの軌道それぞれと、4つの水素原子の1s軌道が重なり合い、σ結合を形成することでメタンの四面体構造が形成されることになる。
 |
 |
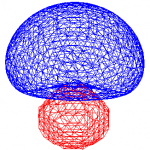 |
| 「Wikipedia:混成軌道」より | 「Wikipedia:メタン」より | sp3混成軌道 |
| ↑1 | 本来、混成軌道は原子価結合法と呼ばれる方法で分子の波動関数を表すために導入されたものであるが、ここでは複数の原子軌道の寄与がある化学結合の電子の重なりを分離して説明するために導入した。一般的な物理化学・量子化学の授業で原子価結合法に基づいて混成軌道が導入されるときは式の形は同じでも考え方がいろいろ違うので注意してください。 |
|---|---|
| ↑2 | C-Hの結合なら、1個の電子が入った水素の1s軌道と、やはり1個の電子が入った上記 |
| ↑3 | なお、上記混成軌道はやみくもに足し引きしてできたわけではない。もともとの各原子軌道は同じ軌道同士を積分すると1(電子の存在確率を全空間で足し合わせると1になる。例: |