ここまでは水素様原子、つまり正電荷がある原子核の周りを電子1個が存在する場合の波動関数の話をしてきたが、通常、水素以外の原子の内部には2個以上の電子が存在する。電子が2個以上あるということは当然、それを表すためのシュレディンガー方程式は違うものになる。シュレディンガー方程式が違うなら、波動関数も水素原子のものとは違うはずで、各々のシュレディンガー方程式を作ってやって解いてやれば波動関数やエネルギーが求められると思うだろう。ところが事情はそう簡単ではない。実は電子が2個以上含まれているような原子についてのシュレディンガー方程式は厳密に解くことができない^*1水素原子の場合は前節のように系のエネルギーや電子の波動関数を式として表すことができたが、電子が2個以上あるとシュレディンガー方程式を解いてエネルギーや波動関数の式として表すことができない。ことが知られている。こうなると、一般の原子についてのシュレディンガー方程式は解けない…ということになるので、何らかの近似を使って考えていくしかない。

さらに、複数の電子があるということは、電子自身の性質のことも考える必要がある。実は電子には、スピンと呼ばれる電子自身の内部自由度があって、２つの状態を取ることができる。この２つの状態は、m_sで表される、電子のスピンを表すための量子数（-1/2,+1/2の２つの値をとりうる）を使って表すことができる。たとえば前節にて水素原子のシュレディンガー方程式の解となる状態（電子状態）はn, l, mの３つの量子数を使って指定できることが示されたが、この３つの量子数だけでは水素原子内の電子がどちらのスピンをとっているかについてはわからない。いま追加されたスピンの量子数m_sを加えて、合計４つの量子数を使うことではじめて、水素原子内部の電子の状態を完全に定めることができる。

組み立て原理

以上のとおり、一般の原子の波動関数は水素様原子とは異なり、それがどのようなものであるかは何らかの近似を入れて計算していかないとわからない。一方、一般の原子といえども水素様原子と根本的に異なっているわけでなく、水素原子でいうところの1s, 2s, 2p, 3s,…といった状態に対応する状態がやはり存在する。そこで一般の原子について考える際もまず1s, 2s, 2p, 3s,…といった波動関数を考え、その上でいくつかの原理に従って複数の電子が順番に詰まっていくと考え、原子の性質を説明していくことになる。これは組み立て原理と呼ばれる。

以上の３つの原則に従って原子の中に電子を入れていったものを考えると、原子スペクトル等、実験で観測される原子の性質を説明できるような電子状態を組み立てることができる。

各原子の電子配置

組み立て原理に従って原子の電子状態を考えるには、まずは各軌道のエネルギーを考え、低い順に電子を入れていくことになる。基本的に、主量子数 n ・軌道量子数 l については量子数が小さい方がエネルギーは小さい一方、磁気量子数 m については値によるエネルギーの変化は小さい。それゆえ、多くの原子では、ｓ軌道よりもｐ軌道が、ｐ軌道よりもｄ軌道がエネルギーが高くなっている。組み立て原理による原子軌道は、このようなエネルギー差がある原子軌道に電子が下から順番に詰まっていくということを意味している。

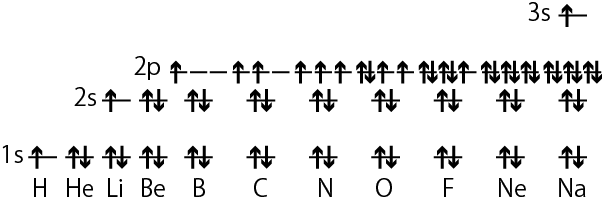
実際に組み立て原理に従って各原子軌道に電子を詰めていく時の例が上の図である。矢印が電子に対応しており、上下の向きが m_s で決まる電子の２つのスピン状態の区別を表す^*2電子の２つのスピンを表す時、このように矢印の向きで表したり、上下の区別、右回り・左回りで区別して説明されることは多いが、実際に電子がどこかの向きを向いていたり、回転していたりするわけではない。なおスピンは物質の磁気的性質に関わっていて、磁石の性質は物質内の沢山の電子が揃って同じタイプのスピンになることで生じる。異なるタイプのスピンの電子が一緒にあるとそれぞれ打ち消し合う。。水素原子では１ｓ軌道に1個だけ電子が入り、ヘリウムだと2個の電子が１ｓ軌道に入るが、パウリの排他原理に従って2個の電子のスピンは逆向きになる。電子を3個持つリチウムは２ｓ軌道に3個目の電子が入り、ベリリウムだと２ｓ軌道まで電子が埋まる。ホウ素、炭素、窒素では２ｐ軌道に電子が詰まっていくが、フントの規則に従ってスピンの向きが同じになるよう別々の２ｐ軌道に電子が入る。そして酸素になってはじめて2個目の電子が２ｐ軌道の１つに入ることになる。

このように電子を順番に詰めていった時、その順番は基本的には量子数 n, l の順番であるが常にこの順番かというとそんなこともなく全体のエネルギーが低くなるように電子は詰まっていく。例えば1s, 2s, 2p, 3s, 3p の順に電子が入っていった後は 3d ではなく 4s となる。これはd軌道に電子を入れるよりも次の周期のs軌道の方がエネルギーが低いためである。

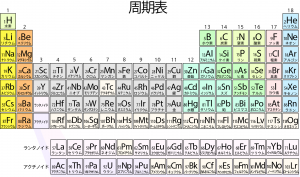
またこうしてみると、組み立て原理による電子の入り方が元素の周期表にも対応していることも分かるだろう。水素、ヘリウムは１ｓ軌道のみに電子を入れるため、周期表の最上段で孤立している。一方、リチウムからネオンまでは、２ｓ、２ｐ軌道に8個の電子を入れていく様子に対応している。また、周期表の縦の列は各軌道への電子の入り方も反映している。水素の列の1族なら、１ｓ（H）、２ｓ（Li）、３ｓ（Na）等、ｓ軌道に1個電子が入った状態になる。2族ならｓ軌道に2個の電子が入る。このように、周期表の縦方向の性質の類似性は、最外殻のｓ軌道、ｐ軌道などへの電子の入り方を反映している。また、周期表の1族，2族が左端、13～18族が右側に分かれて位置しているのも、電子が実際に入る軌道が違っているからということがわかる。（1,2族がs軌道に入るのに対して,　He以外の13~17族はp軌道に入る。またd軌道よりも次の周期のs軌道のエネルギーが低く、4s軌道に電子が入ったあと3d軌道に電子が入るために3~12族は2族と13族の間にある）