水素原子のシュレディンガー方程式と波動関数
それでは、時間に依存しないシュレディンガー方程式を使って水素原子のエネルギーや波動関数を実際に考えてみよう。ここでは1個の水素原子、すなわち原子核と電子でできていて、それぞれが運動しているようなものを考えることにする。
周りに何もなく、光が当たることもなく水素原子が1個だけぽつんと宇宙空間にあるような状態では、水素原子の運動エネルギーや内部の電子の状態いつまでもずっと同じ状態だろう。そういう状態は定常状態と呼ばれ、時間に依存しないシュレディンガー方程式を使って状態やエネルギーを表すことができる。
前節に述べたとおり、時間に依存しないシュレディンガー方程式は$$E\Psi=\hat H\Psi\tag{1.5.4}$$ で表される。水素原子について考える場合は、Eはその水素原子のエネルギー、ψは水素原子の波動関数で、
は水素原子の運動を表すためのハミルトン演算子である。先に述べた量子力学の基本原則において、ハミルトン演算子は古典力学の運動エネルギーと位置エネルギー（ポテンシャルエネルギー）を足し合わせた量の中の運動量 p に対応する項を 
に置き換えて作ったものであると述べた。原子核のまわりを電子が回っているような系なら、その運動エネルギーは電子のエネルギーと原子核のエネルギーで構成されるだろう。つまり $$\frac12m_e v_e^2+\frac12m_n v_n^2\tag{1.6.1}$$ である(me,mnは電子と核の質量、ve,vnは電子と核の速度)。
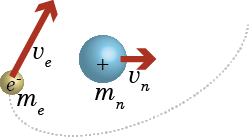
ただ、原子核は電子の1800倍の質量があるため、ほとんど動かない。そこで、原子核は固定されていると考えて、電子の運動エネルギーだけを考えることにする。これはボルン・オッペンハイマー近似と呼ばれる。
また、原子核の正電荷が作る電場は電子の負電荷に影響を及ぼす。このとき電子が感じるポテンシャルエネルギー（位置エネルギー）は $$-\frac{e^2}{4\pi\epsilon_0r}\tag{1.6.2}$$ である。したがって、水素原子の運動エネルギーとポテンシャルエネルギーの和は結局、 $$\frac{p_e^2}{2m_e}-\frac{e^2}{4\pi\epsilon_0r}\tag{1.6.3}$$ となるだろう*1
を使った。
は電子の運動量。念のため。。先の「1.4 量子力学の基本原則」の原則２で述べたように、ここで運動量 p の各方向の成分を に置き換えて作ったものが水素原子の場合の量子力学のハミルトニアンである。結果として、水素原子についての時間に依存しないシュレディンガー方程式は電子の位置を変数とした波動関数ψ(x,y,z) を使って $$ E\Psi(x,y,z)=\left(-\frac{h^2}{8\pi^2 m_e}\left(\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}+\frac{\partial^2}{\partial z^2}\right)-\frac{e^2}{4\pi\epsilon_0r}\right)\Psi(x,y,z)\tag{1.6.4}$$ となる。
この式を解くと*2詳細は触れません。解き方は多くの量子力学・量子化学の教科書に載っています。、水素原子のエネルギーとして $$E_n=-\frac{m_e e^4}{8\epsilon_0^2h^2}\cdot\frac1{n^2} \quad(n=1,2,…)\tag{1.6.5}$$ という式が得られる。n=1,2,…となっているのは、このシュレディンガー方程式は複数の解を持ち、n の値によって解となるエネルギーの値と波動関数の形が違っているということを意味している。
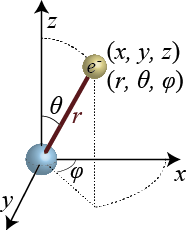
それでは水素原子の波動関数はどうなっているだろうか？元のシュレディンガー方程式(1.6.4)では波動関数は x, y, z という直交座標系の3つの座標を使って電子の位置を表していた。一方、実際に水素原子のシュレディンガー方程式を解いたときは３次元の直交座標系から極座標系に通常変換され、 r, θ, φ という３次元極座標の３つの座標を使って位置を表すことになる。
さらに、n の値で決まるあるエネルギーをとるような波動関数は必ずしも１つではなく、異なる波動関数で表される状態が同じ n で表されるようなエネルギーをとることもあり得る。そのような場合も n に加えて l, m という２つの数（量子数）を使うことで、波動関数がどのような形になるか特定することができる。
これら量子数 n, l, m には、n:主量子数、l:方位量子数、m:磁気量子数という名前がついていて、n, l, m で定められるそれぞれの波動関数には1s, 2s, 2p…といった名前がつけられ、いずれも水素原子のシュレディンガー方程式を満たす。なお、高校の化学・物理で電子の配置を説明するために出てくるＫ殻・Ｌ殻・Ｍ殻といった名前は、主量子数n=1のときがＫ殻、n=2のときがＬ殻といった具合に主量子数nの値に対応した名前である。ただ、大学以降の化学・物理でＫ、Ｌ、Ｍ殻という名前が出てくる場合はかなり少ない*3特性Ｘ線の名称にＫ，Ｌ，Ｍの文字が入っている以外、とんと見かけない気がします。。
電子の存在確率
水素原子の実際の波動関数（水素原子におけるシュレディンガー方程式の解）を下の表に示す。
| 名称 | n | l | m | Ψ (r, θ, φ) = R (r) Y (θ, φ) | |
|---|---|---|---|---|---|
| R (r) | Y (θ, φ) | ||||
| 1s | 1 | 0 | 0 |  |
 |
| 2s | 2 | 0 | 0 |  |
|
| 2p | 2 | 1 | 0 |  |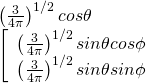
 |
| 2 | 1 | +1 | |||
| 2 | 1 | -1 | |||
得られる波動関数は $$\Psi(r, \theta, \phi)=R(r)Y(\theta, \phi)\tag{1.6.6}$$ のように、r (核-電子間距離)が含まれる部分とそうでない部分の積の形で書くことができるので、表ではr を含む部分、 
と
の関数になっている部分 
を別々に書いてある。
このうち は中心からの距離r による波動関数の大きさの違いに対応しているため動径部分と呼ばれる。 は の値（核→電子のベクトルの向きに対応）によって波動関数の値が変わることに対応するため角度部分と呼ばれる。各々の波動関数のおおまかな形は下図に示したとおりである。
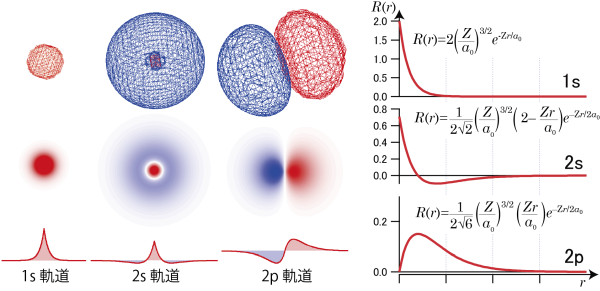
3Dの図は赤色が波動関数が正の値、青色が波動関数が負の値がとるときの等値面になっており、これらを原点を通るような断面で切ったときの値を示しているのが２次元の図。さらにこの原点を通る直線を引いたときの、直線上の波動関数の値をグラフとして表示している。
たとえば１ｓ軌道では、全空間で同じ符号で、原点で最も波動関数の大きさが大きい。２ｓ軌道では の値が正から負に変化することから分かるように、ある球面を境にその内側と外側で波動関数の符号が変わってしまう。２ｐではさらに、角度部分のsinθやcosθの値が角度によって正になったり負になったりする。*4「量子力学の原則」でも述べたように、波動関数は大きさを2乗することで確率を表す量になるが、2乗しない状態では何かの物理量に対応しているわけではない。したがって、ここでの波動関数の正負の符号というのは特に何かに対応しているわけではない。一方、正負の符号が変わる所というのは波動関数の値が０になり、電子の存在確率が０となる。
というわけで、本節では水素原子のエネルギー、波動関数を考えるために、原子核の周りに存在する1個の電子の運動についてのシュレディンガー方程式について考えてきた。電子についての運動方程式を基にしたシュレディンガー方程式の解が上記の1s,2sといった波動関数である。従って、これら波動関数の大きさの2乗は水素原子内で電子がどこにいるかについての確率を意味することになる。また、量子数 n, l, m の組み合わせによって波動関数の形：位置毎の値が異なるということは、量子数によって電子の存在確率が高い場所が違うということでもある。