ここまでは定積条件、定圧条件について話を進めてきたが、この先の話を進める上で、断熱変化についても述べる必要がある。

断熱変化は、外界と熱のやりとりがない条件で起きる変化である。熱のやりとりがないので、熱力学第一法則 ∆U=q+w において q=0 であることから、断熱条件で系にされた仕事はすべて内部エネルギーの変化となる。

理想気体の内部エネルギーが だったことからもわかるように、内部エネルギーが大きくなると温度は上昇し、内部エネルギーが小さくなると温度は低下する。従って、断熱条件で系に仕事をして圧縮した場合は温度が上昇し( ∆U=w>0 )、系が仕事をしながら膨張した場合は温度が低下( ∆U=w≤0 )することになる。

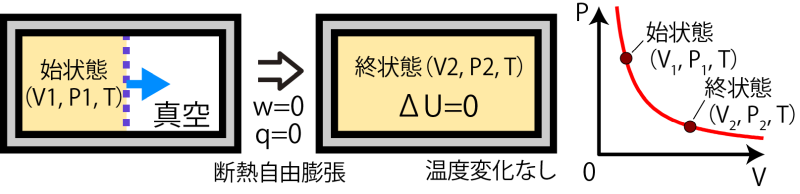
　一方、もし系が仕事をされることなく気体の体積が変わったとすると、温度は変化しない。たとえば、断熱容器の中に壁を作り、片方の区画のみに気体を詰めた状態から壁を突然取り払ったとする（壁を取り払う仕事は０とする）。この場合、系がされる仕事はない（ w=0 , 外力0を受けてピストンを移動しても系がされる仕事は０）ので温度は変わらない（ ΔU=q+w=0 ）ことになる。これは断熱自由膨張と呼ばれる。

なお、圧縮や膨張過程を考える際、始状態と終状態は各々平衡状態を想定しているため系内部の圧力は均一であり、系としての圧力を決めることができるが（PV図上にプロット可能である）、自由断熱膨張や、そのほか一般の断熱膨張・断熱圧縮の途中の状態は非平衡状態であり内部の圧力が均一でないため系としての圧力は決められず、PV図上にプロットできるような状態ではない。一方、次項では、操作の途中もPV図にプロットできるように平衡状態を維持しながら断熱操作を行う場合の挙動、可逆断熱過程について考える。

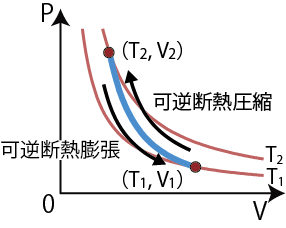
可逆断熱変化のP-V挙動

断熱変化では、操作によって温度、体積の両方が変化する。特に可逆断熱過程、すなわち平衡状態を維持しながら内圧と外圧が同じ状態を維持しながら、外部と熱の出入りがなくゆっくりと操作する過程がPV図上のどこを通るかを考えることにする。

まず、断熱過程は熱の出入りがないので、熱力学第一法則から

である。ここで、経路上の各点で微小な体積変化 dV を起こしたときの仕事は であるので、 PV=nRT と組み合わせると内部エネルギー変化は$$dU=-PdV=-\frac{nRT}{V}dV \tag{5.6.2}$$ となる。また、温度変化に伴う内部エネルギー変化が比熱だったので、経路上の各点で$$dU=C_V dT \tag{5.6.3}$$も成立している。そこで、１モルあたりの定積熱容量^*1 n=1 における C_V をとしてこれらをまとめると、 $$\begin{align}C_{V,m} dT &= -\frac{RT}{V} dV \\ \frac{C_{V,m}}{T}dT &= -\frac{R}{V}dV \tag{5.6.4}\end{align}$$ も成り立っていると考えられるだろう。この式は変数分離型の微分方程式と呼ばれるもので、両辺をそれぞれの変数で積分することで解くことができる。操作の始点(T₁, V₁)から終点(T₂, V₂)まで積分するならば、$$\begin{align}\int_{T_1}^{T_2}\frac{C_{V,m}}{T}dT&=\int_{V_1}^{V_2} -\frac{R}{V}dV \\ C_{V,m}\int_{T_1}^{T_2}\frac{1}{T}dT&=-R\int_{V_1}^{V_2}\frac{1}{V}dV \\ C_{V,m} ln \frac{T_2}{T_1}&=R ln\frac{V_1}{V_2} \tag{5.6.5}\end{align}$$ が出てくる^*2という積分公式があった。序章で示したとおり、log_eはlnと表記する。。これをもうすこし変形してやると、$$\frac{T_2}{T_1}=\left(\frac{V_1}{V_2}\right)^{\frac{R}{C_{V,m}}} $$ $$ \rightarrow T_1 V_1^{\frac{R}{C_{V,m}}}=T_2 V_2^{\frac{R}{C_{V,m}}} \tag{5.6.6}$$ なので、可逆断熱過程では

が成り立っていることが分かる。さらに$$\gamma =\frac{C_P}{C_V} \tag{5.6.7}$$とおき、物質量 n=1 における状態方程式 と定容・定積熱容量の関係 を使うと、$$TV^{\frac{R}{C_{V,m}}}=\frac{P}{R} V^\left(\frac{R}{{C_{V,m}}}+1\right)=\frac{P}{R}V^{\frac{{C_{V,m}}+R}{{C_{V,m}}}}=\frac{P}{R} V^{\left(\frac{C_P}{C_V}\right)}=\frac{P}{R} V^{\gamma} \tag{5.6.8}$$となる。気体定数 R の値は常に変わらないので、

であることもわかる。この関係はポアソンの法則と呼ばれ、可逆断熱過程がPV図上のどこを通るかについて教えてくれるものである。

 [+]

References

↑1	n=1 における CV
↑2	という積分公式があった。序章で示したとおり、logeはlnと表記する。