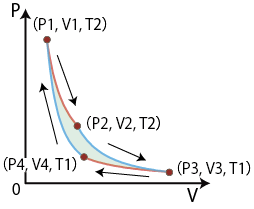
カルノーサイクル
高温の熱源から熱を取り入れて低温の熱源に放出させる過程で熱を仕事に変える働きを周期的に行う装置が熱機関である。カルノーサイクルはフランスのカルノーが熱機関の研究のために19世紀に導入した熱機関であり、理論上最も効率が良い熱サイクルとして知られている。カルノーサイクルは高温熱源、および低温熱源に接して行う2つの等温可逆過程と2つの断熱可逆過程、計4つの過程からなっている。
過程1:高温熱源と接して等温可逆膨張(P1,V1,T2)→(P2,V2,T2)
過程2:断熱可逆膨張(P2,V2,T2)→(P3,V3,T1)
過程3:低温熱源と接して等温可逆圧縮(P3,V3,T1)→(P4,V4,T1)
過程4:断熱可逆圧縮(P4,V4,T1)→(P1,V1,T2)
カルノーサイクルの熱効率
それでは実際にカルノーサイクルの熱効率を計算してみよう。カルノーサイクルは4つの過程からなるのでそれぞれの過程における熱の出入りと仕事について計算すると以下のようになる*1過程2,4の仕事は可逆過程の途中の各平衡状態で dU=CvdT が成り立つところから出している。 。
過程2:q=0, w_2=\Delta U=\int_{T_2}^{T_1} C_V dT=C_V (T_1-T_2) \\
過程3:\Delta U=0, q_1=-w_3=\int PdV=\int_{V_3}^{V_4} \frac{nRT_1}{V} dV =nRT_1 ln \frac{V4}{V3} \\
過程4:q=0, w_4=C_V (T_2-T_1) $$
カルノーサイクル全体で系がされた仕事は4つの過程で系がされた仕事の合計であるので、
$$\begin{align}w_{cycle} &= w_1+w_2+w_3+w_4\\
&=-nRT_2 ln \frac{V_2}{V_1}+C_V (T_1-T_2 )-nRT_1 ln \frac{V_4}{V_3}+C_V (T_2-T_1 ) \\
&= -nRT_2 ln \frac{V_2}{V_1}-nRT_1 ln \frac{V_4}{V_3} \tag{6.3.1}\end{align}$$
ここで過程2と4は断熱可逆過程ということで ![]() 一定→
一定→![]() 一定なので
一定なので
$$ T_2^{\frac{C_V}{R}} V_2= T_1^{\frac{C_V}{R}} V_3, T_1 ^{\frac{C_V}{R}} V_4= T_2^{\frac{C_V}{R}} V_1 \tag{6.3.2}$$
から
$$ \frac{T_2^{\frac{C_V}{R}}}{T_1^{\frac{C_V}{R}}} =\frac{V_3}{V_2} , \frac{T_1^{\frac{C_V}{R}}}{T_2^{\frac{C_V}{R}}} =\frac{V_1}{V_4}$$ $$\rightarrow \frac{V_3}{V_2} =\frac{V_4}{V_1} \rightarrow \frac{V_3}{V_4} =\frac{V_2}{V_1} \tag{6.3.3}$$ となり (Cvは定容熱容量)、
$$w_{cycle}==-nRT_2 ln \frac{V_2}{V_1}-nRT_1 ln \frac{V_1}{V_2}=-nR(T_2-T_1 )ln \frac{V_2}{V_1} \tag{6.3.4}$$
となる。また、熱効率 η は系に供給された熱 q2 と系が外部にした仕事( -wtotal )の比なので
となる。この結果は、カルノーサイクルの熱効率は低温・高温の熱源の温度のみに依存することを意味している。また、T1が 0 K でない限り熱効率は必ず 1 (つまり100%) より小さいが、これはトムソンの原理による熱力学第二法則、すなわち「熱源から得た熱をすべて仕事に変えるような熱機関は存在しない」に対応している。
カルノーサイクルとエントロピー変化
熱機関におけるエントロピー変化も見ていくことにする。カルノーサイクルの過程1〜4におけるエントロピー変化をそれぞれ∆S1~∆S4とすると、まず、断熱可逆過程のエントロピー変化は0であるため、カルノーサイクル内の断熱可逆:過程2, 過程4でのエントロピー変化も ∆S2=∆S4=0 である。また、カルノーサイクルの熱効率の式の導出の際出てきた ![]() から*2
から*2![]()
という関係が導かれるが、これはカルノーの定理と呼ばれている。また、この式の各項は等温可逆過程1,3のエントロピー変化に対応しているので、∆S1+∆S3=0 となる。結果として
となり、カルノーサイクルでは仕事を行ってもエントロピーの変化はない。
一方、熱機関に不可逆過程が含まれる場合、熱機関サイクルとしてのエントロピー変化が0になることはない。たとえば、もしカルノーサイクル内の等温過程の1つが不可逆だったとすると、その過程でやり取りされる熱 q不可逆は可逆過程だった場合やり取りされる熱 q可逆よりも必ず小さく*3可逆過程のエントロピー変化は q可逆 ⁄ T可逆 = ∆S であるが、不可逆過程のエントロピー変化は ∆S > q不可逆 ⁄ T不可逆 であるので等温過程なら ∆S = q可逆 ⁄ T > q不可逆 ⁄ T だろう。、この熱機関サイクルのエントロピー変化は
$$\frac{q_{可逆}}{T_{可逆}}+\frac{q_2}{T_2}=0>\frac{q_{不可逆}}{T_{不可逆}}+\frac{q_2}{T_2} \tag{6.3.8}$$ となる。これをより一般化して、1つの熱機関のサイクルを構成する全ての過程でやりとりされる熱について書いた式として
がある。なお、この式をクラウジウスの不等式と呼ぶ教科書も多い*4多くの熱力学の教科書でこの式がクラウジウスの不等式として紹介されている。先に紹介した ΔS≧q/T とは式の内容・意味共に異なるので注意。。