化学反応にはエンタルピー変化が正か負かによって吸熱反応と発熱反応があることは前節で触れた。世の中で起きている化学反応は必ずしも発熱反応だけではなく、吸熱反応も起きている。例えば塩が水に溶ける時の溶解のエンタルピー変化は 3.8 kmol/J であり、吸熱反応であるので、溶解によって系としてはエネルギーが高い方向に、不安定化していることになるが、それでも塩は水に溶けるわけである。つまり、化学反応の進行にはエンタルピーや内部エネルギー以外の要素も関与していることになる。化学反応の進行に関与しているもう1つの量として、系の乱雑さを表す量であるエントロピーと呼ばれる量がある。エントロピーにはミクロに見た場合とマクロに見た場合でいくつかの定義があるが、いずれも同じことを意味していることを次節では見ていくことにする。*1ここでの説明は概ね現代物理化学(化学同人)に準拠しているのでそちらも参照のこと。
ボルツマンのエントロピー(統計力学におけるエントロピー:個々の粒子を考える)
はじめに、統計力学によるエントロピーの定義であるボルツマンのエントロピーについて紹介する。ボルツマンのエントロピーは、ミクロな量である1個1個の分子が取りうる状態の数から定義される乱雑さを表す量になっており、エントロピーSは
と定義される。ただし W は粒子の取りうる場合の数、kB はボルツマン定数である。しかしこれだけ見せられても、場合の数って何だ?よくわからないなぁ…と思うだろう。…というわけで、粒子の取りうる場合の数とはどのようなものか、例を見ていく。
まずは2個の同じ分子 a, b を異なる容器 A, B に入れることを考える。この場合、分子 a, b の入り方としては4通りがあるが、a, b が同じ分子で区別できるようなものではないとすれば、 A, B に1個ずつ分子が入っている2つの状態は同じ状態である*2容器AとBは区別できるので、A だけに入っている状態、Bだけに入っている状態は別の状態である。。この場合、2個の分子がAのみに入っている状態(1つ)よりも、A, Bに1個ずつ入っている状態(2つ)の方が場合の数が多いことになる。
例:同じ容積の2個の容器A,Bに2個の気体分子が入るとき、分子a,bの入り方は4とおり
| Aのみ | A[a,b]B[_,_] | 1通り |
| A,Bに1個ずつ | A[_,b]B[a,_], A[a,_]B[_,b] | 2通り(同じ状態) |
| Bのみ | A[_,_]B[a,b] | 1通り |
同様に、10個の分子を A, B に入れた時を考えると、片方の箱だけにすべての分子が入っているような状態よりも、A, B に5:5の比率で分子が入っている場合の数が 252 倍も大きい。上の定義で出てきたエントロピーの W の所の場合の数は、ここで出てきた場合の数である。したがって、分子が容器Aだけに入っている状態に比べて、5:5で分子が入っている状態の方がエントロピーが大きいことになる。
10個の分子の入り方
| A:B | 10:0 | 9:1 | 8:2 | 7:3 | 6:4 | 5:5 | 4:6 | 3:7 | 2:8 | 1:9 | 0:10 |
| 場合の数 | 1 | 10 | 45 | 120 | 210 | 252 | 210 | 120 | 45 | 10 | 1 |
→Aに10個分子が入った状態より5:5の割合になる状態のほうがエントロピーが大きい:とりうる状態の数が多い、より乱雑な状態
さらに分子が多くなると、より均等に分子が存在することになる。アボガドロ数( 6.0×1023 )程度もの分子が容器に入っている場合は、もはや片方の容器のみに分子が入るような確率は極めて低くなり、2つの容器に均等に分子が入った状態の場合の数が大きくなる。それゆえ2つの容器に均等に分子が入った状態がエントロピーが大きな状態である。見方を変えるならば、分子は場合の数が大きい状態、つまり乱雑な状態になりやすい…というふうに言い換えることもできるかもしれない。
クラウジウスのエントロピー(熱力学におけるエントロピー:個々の分子を考えない)
次に、クラウジウスによるエントロピーの定義を紹介しよう。クラウジウスによるエントロピーの定義は、
となり、エントロピーの絶対値ではなく変化量が定義されている。すなわち、ある可逆過程が起きた時、系を出入りする熱を温度で割ったものがその可逆過程における系のエントロピー変化となる。
たとえば、等温可逆過程(温度一定になるように外界と熱のやりとりをしながら内圧と外部からの力が釣り合うようにゆっくりと平衡状態を保ったまま体積を変化させる)では定義通り、![]() が系のエントロピー変化である。
が系のエントロピー変化である。
一方、断熱可逆過程(系と外界の熱のやりとりがなく、内圧と外部からの力が釣り合うようにゆっくりと平衡状態を保ったまま体積を変化させる)では、熱のやりとりがない( q=0 )のでΔS=0 となる。
そして、この定義式は可逆過程(平衡状態を保ったままゆっくりと体積・温度・圧力などが変化するような過程)でしか成り立たない。
等温可逆膨張における2種類のエントロピー定義と体積・圧力の関係
これら2つのエントロピー、ぱっと見た感じ全然違うもののように見える。そこで、ここで出てきた2つの定義によるエントロピーから導かれる結果が同じになることを、理想気体の等温可逆膨張を例に確認してみることにしよう。
クラウジウスの定義にて考える
はじめにクラウジウスによるエントロピーの定義を使って、等温可逆過程のエントロピーと体積・圧力の関係を調べてみる。等温可逆過程の場合、温度が変わらないということは内部エネルギー変化はゼロである( ∆U=0 )。熱力学第一法則(∆U=q+w)と理想気体の状態方程式(PV=nRT)を使うと、体積が V1 → V2 、圧力が P1 → P2 になるような等温可逆過程で系が受け取る熱は$$q=-w=\int P dV= \int_{V_1}^{V_2} \frac{nRT}{V} dV = nRT ln \frac{V_2}{V_1} = nRT ln \frac{\frac{nRT}{P_2}}{\frac{nRT}{P_1}}=nRTln \frac{P_1}{P_2} \tag{6.1.3}$$ となるので、エントロピー変化は$$\Delta S=\frac{q}{T} = nR ln \frac{V_2}{V_1}= nR ln \frac{P_1}{P_2} \tag{6.1.4}$$ となる。
ボルツマンの定義にて考える
次に、ボルツマンの定義によるエントロピーを使って等温可逆過程について考えてみることにしよう。
まず、等温可逆過程によって、体積が V1 → V2 に変化したとしよう。このとき、気体分子1個が膨張後に V2 (容器内)にいる確率は1である(容器内のどこかに必ず分子が存在する)。一方、気体分子1個が膨張後に元のV1 の範囲(元の領域)にいる確率は V1 / V2 となるだろう。容器内に n モルの分子があってそれぞれ独立なら、V1 にいる確率と、V2 にいる確率の比はちょうど分子nNA 個が V1 と V2 の領域にいる場合の数の比となり、
$$\frac{分子 n モルがV_2にいる場合の数}{分子nモルがV1にいる場合の数}=\left(\frac{1}{\frac{V_1}{V_2}}\right)^{nN_A}=\left(\frac{V2}{V1}\right)^{nN_A } \tag{6.1.5}$$となる。
エントロピー変化は場合の数のloge についての差であるので、ここで求めた場合の数の比を代入することができ、$$\Delta S=k_B ln W_2-k_B ln W_1=k_B ln \frac{W_2}{W_1} =nN_A k_B ln \frac{V_2}{V_1}=nR ln \frac{V_2}{V_1} \tag{6.1.6}$$となる。
これはクラウジウスによる定義を使った場合の結果と同じである。
クラウジウスの定義とボルツマンの定義、違って見えるエントロピーの2つの定義は実際には等価ということが実感できたのではないだろうか?
不可逆過程のエントロピー変化
ここまでで出てきた熱力学におけるエントロピーの特徴について簡単にまとめるとともに、計算方法について考えてみよう。ここからはクラウジウスによる定義に基づいて話を進める。
まず、エントロピーは圧力や体積、内部エネルギーやエンタルピーなどと同様、系の状態が定まると値がただ1つに定まるような物理量、状態変数である。
次に、可逆過程において、エントロピー変化について ![]() という式が成立する。
という式が成立する。
可逆過程でない過程(不可逆過程)では上記等式は成立しないが、世の中には不可逆過程が溢れている。不可逆過程では、上記の等式は成立せず、![]() となりこれらをまとめた$$\Delta S\geq \frac{q}{T} \tag{6.1.7}$$ はクラウジウスの不等式と呼ばれることがある。*3野本が確認した限り、アトキンス物理化学、現代物理化学、物理化学Ⅱ(妹尾) はこの式をクラウジウスの不等式と呼んでいる。一方、他の式(
となりこれらをまとめた$$\Delta S\geq \frac{q}{T} \tag{6.1.7}$$ はクラウジウスの不等式と呼ばれることがある。*3野本が確認した限り、アトキンス物理化学、現代物理化学、物理化学Ⅱ(妹尾) はこの式をクラウジウスの不等式と呼んでいる。一方、他の式( ![]() )をクラウジウスの不等式と呼ぶ教科書(熱力学の教科書に多い。Wikipediaもこちら)もあるので注意が必要である。
)をクラウジウスの不等式と呼ぶ教科書(熱力学の教科書に多い。Wikipediaもこちら)もあるので注意が必要である。
そんな過程におけるエントロピー変化はどうやって計算したらよいだろうか?? ここで鍵となるのが「エントロピーは状態変数である」点である。圧力や体積、内部エネルギーと同様、エントロピーは状態変数なので、状態が定まれば*4圧力、温度、体積、物質量といった系を定めるための状態変数の組が決まればエントロピーの値は自動的に決まる。そして、可逆過程におけるエントロピー変化は上記 ![]() 式で計算ができる。ならば、不可逆過程の始状態と終状態の間を結ぶ可逆過程を適当に考えてやって、そちらのエントロピー変化を考えてやれば、それは求めたい不可逆過程におけるエントロピー変化と等しくなるというわけである。このときの経路は可逆過程でありさえすればなんでもよい。うまい具合にエントロピーは系の状態によって決まる量なので、変化前、変化後の状態さえ定まっていれば、どの経路でエントロピーを計算しても同じ∆Sの値になるようになっている。
式で計算ができる。ならば、不可逆過程の始状態と終状態の間を結ぶ可逆過程を適当に考えてやって、そちらのエントロピー変化を考えてやれば、それは求めたい不可逆過程におけるエントロピー変化と等しくなるというわけである。このときの経路は可逆過程でありさえすればなんでもよい。うまい具合にエントロピーは系の状態によって決まる量なので、変化前、変化後の状態さえ定まっていれば、どの経路でエントロピーを計算しても同じ∆Sの値になるようになっている。
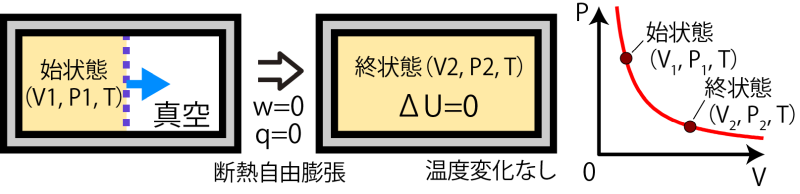
計算例:断熱自由膨張
例として下の図のような断熱自由膨張を考える。これまで何度か出てきたように、断熱自由膨張では容器の中で壁を隔てて気体と真空になっている状態から、突然壁を外して全体で均一な状態になるような過程である。この時、壁の外は真空なので、系に外部から加わる力はなく、したがって系にされる仕事もない( w=0 )。また、断熱変化なので熱の出入りもない( q=0 )。しかし、断熱変化だからといってこの時のエントロピー変化を ![]() としてしまってはいけない。断熱自由膨張で壁を外した直後というのは元の領域にしか気体がない不均一な状態であり、この過程は非平衡状態を経由する不可逆過程であるので
としてしまってはいけない。断熱自由膨張で壁を外した直後というのは元の領域にしか気体がない不均一な状態であり、この過程は非平衡状態を経由する不可逆過程であるので ![]() 式は使えないわけである。
式は使えないわけである。
それではこの過程のエントロピーはどうやって求められるかといえば、始状態(V1, P1, T)から終状態(V2, P2, T)に至る可逆過程を考え、その可逆過程のエントロピー変化を考えればよい*5この過程はw=0、 q=0 なので ΔU=0。したがって温度変化はない。。断熱自由膨張では内部エネルギーが変化せず、温度が変化しないことから、(V1, P1, T)→(V2, P2, T)の等温可逆過程のエントロピー、すなわち$$\Delta S=\frac{1}{T} \int_{V_1}^{V_2} P dV= nR ln \frac{V_2}{V_1} \tag{6.1.8}$$が断熱自由膨張のエントロピー変化に対応するものとなる。
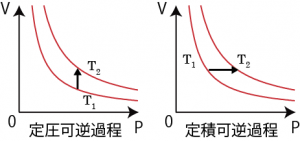
定積可逆過程・定圧可逆過程のエントロピー変化
以上のようにエントロピーは始状態と終状態を結ぶ可逆過程の経路を考えてそのエントロピーを計算すればよく、従ってどんな過程も等温可逆過程( ΔS=q/T )と断熱可逆過程( ΔS=0 )を組み合わせることで計算可能であるが、定積可逆過程、定圧可逆過程のエントロピー計算の方法も紹介しておく。
体積一定の定積過程や圧力一定の定圧過程も、内圧と外圧が釣り合う平衡状態を保ったままゆっくりと(準静的に)仕事をして温度温度上昇させれば可逆過程になる。まずは定積可逆過程の場合を考えると、定積モル比熱の関係式、dq=dU=CV dT は定積可逆過程の経路上の各々の平衡状態にて成り立っている。また、これらの平衡状態から微小な定温可逆過程が起きる場合エントロピー変化は![]() となる*6微小な定温可逆変化のあとに微小な断熱可逆変化をさせれば体積を変えずに微小な温度変化が可能となり、そのときのエントロピー変化も
となる*6微小な定温可逆変化のあとに微小な断熱可逆変化をさせれば体積を変えずに微小な温度変化が可能となり、そのときのエントロピー変化も![]() となる…と考えてもよいだろう。。したがって
となる…と考えてもよいだろう。。したがって![]() を始点から終点までの温度で積分した、
を始点から終点までの温度で積分した、
が定積可逆過程のエントロピー変化である。
同様に、定圧可逆過程についても、各々の平衡状態で dq=CP dTが成りたっていることから、これを始点から終点温度まで積分してやればエントロピー変化となり、
となる。なお、これらの結果はいずれも等温可逆過程、断熱可逆過程を組み合わせて計算したときの値とも等しいので、試しに計算してみてほしい。
混合エントロピー
物質が混合される時もエントロピー変化が生じるので混合エントロピーと呼ばれる。
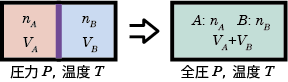
例として気体分子の相互作用がなく温度 ( T ) も圧力 ( P )も等しい、異なる2種類の気体A(物質量 nA, 体積 VA), B (物質量 nB, 体積 VB )を混合する場合を考える。
この時、混合によって体積はVA, VBから、VA + VBに変化するので、混合後の気体A,B のモル分率をそれぞれ ![]() とすると、分圧は
とすると、分圧は![]() となる。ゆえに、各々のエントロピー変化については$$A:\Delta S_A=n_A R ln\frac{V_A+V_B}{V_A}=n_A R ln\frac{P}{X_A P}=n_A R ln\frac{1}{X_A} \tag{6.1.11}$$ $$B:\Delta S_B=n_B R ln\frac{V_A+V_B}{V_B}=n_B R ln\frac{P}{X_B P}=n_B R ln\frac{1}{X_B} \tag{6.1.12}$$となるので、混合エントロピーは
となる。ゆえに、各々のエントロピー変化については$$A:\Delta S_A=n_A R ln\frac{V_A+V_B}{V_A}=n_A R ln\frac{P}{X_A P}=n_A R ln\frac{1}{X_A} \tag{6.1.11}$$ $$B:\Delta S_B=n_B R ln\frac{V_A+V_B}{V_B}=n_B R ln\frac{P}{X_B P}=n_B R ln\frac{1}{X_B} \tag{6.1.12}$$となるので、混合エントロピーは
&=n_A R ln\frac{1}{X_A}+n_B R ln\frac{1}{X_B} \\
&=-R(n_A ln X_A+n_B ln X_B ) \tag{6.1.13}\end{align}$$
となる。
つまり、混合によるエントロピー変化は各成分の体積変化に由来しており、VA→VA+VBおよびVB→VA+VBの体積変化のエントロピー変化の和を全体のエントロピー変化として、それらをモル分率の形で書き表したものになっている。
| ↑1 | ここでの説明は概ね現代物理化学(化学同人)に準拠しているのでそちらも参照のこと。 |
|---|---|
| ↑2 | 容器AとBは区別できるので、A だけに入っている状態、Bだけに入っている状態は別の状態である。 |
| ↑3 | 野本が確認した限り、アトキンス物理化学、現代物理化学、物理化学Ⅱ(妹尾) はこの式をクラウジウスの不等式と呼んでいる。一方、他の式( |
| ↑4 | 圧力、温度、体積、物質量といった系を定めるための状態変数の組が決まれば |
| ↑5 | この過程はw=0、 q=0 なので ΔU=0。したがって温度変化はない。 |
| ↑6 | 微小な定温可逆変化のあとに微小な断熱可逆変化をさせれば体積を変えずに微小な温度変化が可能となり、そのときのエントロピー変化も |