次に、系に加える熱と温度の関係を見ていくことにする。
系の温度を上げるために必要な熱量を教えてくれる物理量が熱容量である。
熱が q だけ入ることで ΔT だけ系の温度を上がる場合、系の温度を単位温度(1度)上げるのに必要な熱は $$\frac{q}{\Delta T} \tag{5.4.1}$$ と考えることができるだろう。定積条件(体積一定)の場合、系を出入りする熱は内部エネルギーの変化 ( q=ΔU )に対応していたので、$$\frac{\Delta U}{\Delta T} \tag{5.4.2}$$ という量が系の温度を単位温度(1度)だけ上げるために必要な熱量である。これを微分として表した
は定容熱容量、または定積熱容量と呼ばれる。
同様に定圧条件(圧力一定)の場合、系を出入りする熱はエンタルピー変化、q=ΔH に対応している。そこで、
は定圧熱容量と呼ばれている。
理想気体の場合、状態方程式 PV=nRT とエンタルピーの定義式、H=U+PV をもとに、$$H=U+nRT \tag{5.4.5}$$として、これをTで微分すれば、$$\frac{dH}{dT}=\frac{dU}{dT}+nR \tag{5.4.6}$$すなわち
という式を導くことができる。これが、理想気体における定積熱容量と定圧熱容量の関係式である。
単原子分子理想気体の熱容量
ここで、気体分子運動論を思い出してみると、理想気体の分子一個の運動エネルギーは1方向あたりの値が ![]() で、全体では$$E_{trans}=\frac32 k_B T=\frac32 \frac{R}{N_A} T \tag{5.4.8}$$と書き表された。このときの分子は内部構造を考えないことにしていたので、この値が分子1個あたりの内部エネルギーである。従って、分子1個あたりの比熱は$$\frac{dU}{dT}=\frac{E_{trans}}{dT}=\frac32 \frac{R}{N_A} \tag{5.4.9}$$ となる。また、分子同士の相互作用も考えなかったので、物質量 n の内部エネルギーは nNA 個の分子の運動エネルギーの和ということになり、$$U=nN_A E_{trans}=\frac32 nRT \tag{5.4.10}$$となる。また、この場合の定積熱容量は
で、全体では$$E_{trans}=\frac32 k_B T=\frac32 \frac{R}{N_A} T \tag{5.4.8}$$と書き表された。このときの分子は内部構造を考えないことにしていたので、この値が分子1個あたりの内部エネルギーである。従って、分子1個あたりの比熱は$$\frac{dU}{dT}=\frac{E_{trans}}{dT}=\frac32 \frac{R}{N_A} \tag{5.4.9}$$ となる。また、分子同士の相互作用も考えなかったので、物質量 n の内部エネルギーは nNA 個の分子の運動エネルギーの和ということになり、$$U=nN_A E_{trans}=\frac32 nRT \tag{5.4.10}$$となる。また、この場合の定積熱容量は
定圧熱容量は
となる。
2原子分子理想気体の場合
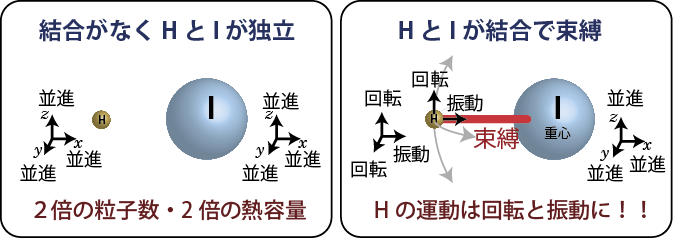
次に、分子が内部構造を持っていたとして、2原子分子理想気体を考える。もし分子を構成する2個の原子が自由に動き回っていたとするならば、単純に2倍の粒子が存在することになるのでその比熱は ![]() となるだろう。しかし、2原子分子では2個の粒子は自由に動き回ることができず束縛されている。
となるだろう。しかし、2原子分子では2個の粒子は自由に動き回ることができず束縛されている。
例としてヨウ化水素、HI分子について考えてみると、この分子ではヨウ素の原子量は水素の原子量の約127倍と重いため、概ねヨウ素原子を中心にして回転している。この場合、水素原子がヨウ素原子方向に動こうとしても、化学結合のために自由に動くことができない。たとえば、水素原子がヨウ素原子方向に動こうとする運動エネルギーというのも、実は化学結合というバネで結びつけられた2個のおもり(原子)の振動エネルギーになってしまう。同様に、水素ーヨウ素方向と垂直な2方向に水素原子が動こうとする運動エネルギーも実は、ヨウ素原子を中心とした回転のエネルギーになってしまうので、気体分子運動論で扱っていたような xyz 方向の自由な運動エネルギーというのはヨウ素原子のxyz 方向の運動しかないということになる。
ヨウ化水素以外の2原子分子の場合も、2個の原子の位置を重心位置 ( xc, yc, zc )と回転角 ( θ, φ )、原子間距離 ( r ) でという6つのパラメータ(変数)で表すことができることからわかるように、xyz 方向に自由に動けるパラメータは2個の原子がもともと持っていた6つの自由度( x1, y1, z1, x2, y2, z2 ) のうち3つ( xc, yc, zc ) しかなく、2つ ( θ, φ )は回転の、もう1つ( r ) は振動のエネルギーになってしまう。
それでは、このような2原子分子からなる理想気体に熱が加わった時どうなるか?
単原子分子理想気体では熱によって1方向あたり ![]() という運動エネルギーを持つという説明をした。回転や振動のエネルギーになってしまうとはいえ、それらも力学的な運動のエネルギーには変わりないので、2原子分子理想気体でも1方向あたり
という運動エネルギーを持つという説明をした。回転や振動のエネルギーになってしまうとはいえ、それらも力学的な運動のエネルギーには変わりないので、2原子分子理想気体でも1方向あたり ![]() のエネルギーが分配されると考えても良いと思うかもしれない。
のエネルギーが分配されると考えても良いと思うかもしれない。
ところが、実際には量子論のせいでそうはならない。2.2分子のシュレディンガー方程式の項目において、バネにつながれたおもりの振動は ![]() というエネルギーを、2原子分子の回転は
というエネルギーを、2原子分子の回転は ![]() というエネルギーを持つという話をした。ここで、各々のエネルギーは量子数 v または J の値で決まるような飛び飛びの値となる。そして、振動の場合、v=0 とv=1のエネルギー差は
というエネルギーを持つという話をした。ここで、各々のエネルギーは量子数 v または J の値で決まるような飛び飛びの値となる。そして、振動の場合、v=0 とv=1のエネルギー差は ![]() あるが、このエネルギー、実は入ったきた熱のエネルギー
あるが、このエネルギー、実は入ったきた熱のエネルギー![]() よりかなり大きいので入ってきた熱エネルギーをエネルギーの高い振動状態に分配することができないのである*1回転のエネルギーについては分配可能であるが、低温になると分配できなくなるので比熱が変わる。。
よりかなり大きいので入ってきた熱エネルギーをエネルギーの高い振動状態に分配することができないのである*1回転のエネルギーについては分配可能であるが、低温になると分配できなくなるので比熱が変わる。。
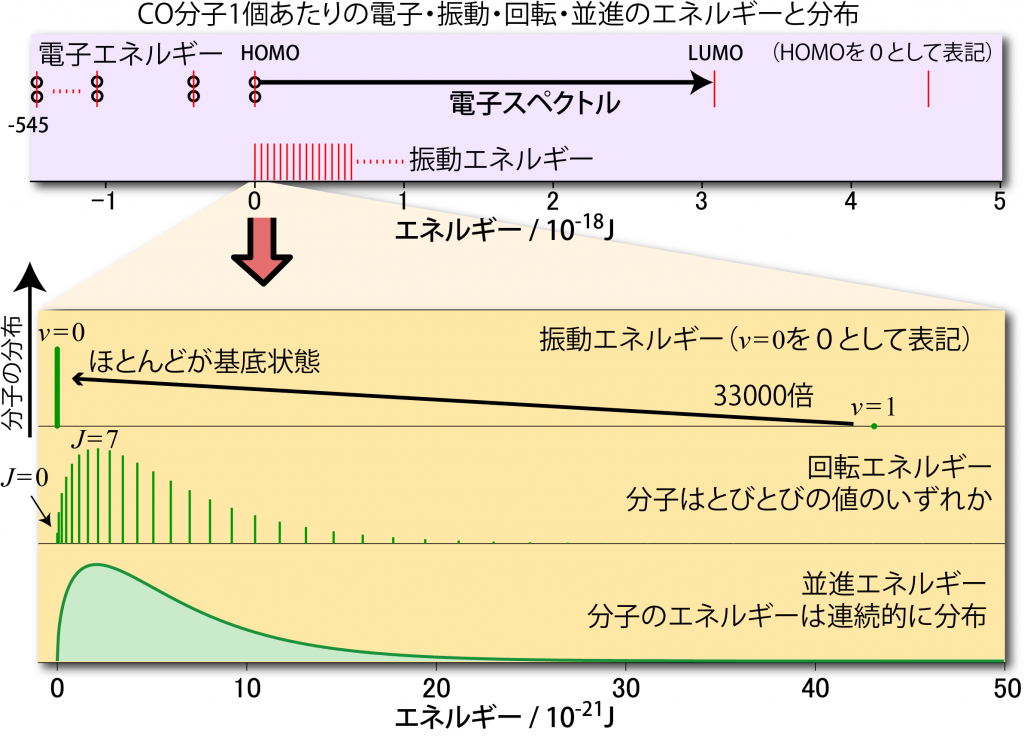
例としてCO分子の場合のイメージを下に図として示した。この図はCO分子の電子・振動・回転・並進エネルギーを並べて描いたもので、電子基底状態かつ振動・回転・並進のエネルギーが基底状態のときのエネルギーを 0 J として、各々のエネルギー準位を比較できるように描いたものだ。
このうち一番上の段は電子のエネルギーと振動エネルギーの比較で、HOMO→LUMO間のエネルギーに比べて振動のエネルギー間隔:![]() がだいぶ小さいのがわかる。下の段は300Kにおける振動・回転・並進の各エネルギーをとる分子の割合の比較で、並進のエネルギーは連続的なので300Kのエネルギー分布関数そのままである。回転のエネルギーはとびとびの値を持つが、ある程度間隔が小さいのでエネルギー分布関数を再現できるが、振動のエネルギーになると、v=1 の準位ですらエネルギー分布関数のピークよりはるか高いところにある。つまり、少々熱を加えたところで振動のエネルギーは励起できないというわけである。
がだいぶ小さいのがわかる。下の段は300Kにおける振動・回転・並進の各エネルギーをとる分子の割合の比較で、並進のエネルギーは連続的なので300Kのエネルギー分布関数そのままである。回転のエネルギーはとびとびの値を持つが、ある程度間隔が小さいのでエネルギー分布関数を再現できるが、振動のエネルギーになると、v=1 の準位ですらエネルギー分布関数のピークよりはるか高いところにある。つまり、少々熱を加えたところで振動のエネルギーは励起できないというわけである。
その結果、2原子分子では加えられた熱エネルギーは振動以外の5つのパラメータに分配され、定積比熱は単原子理想気体よりも大きくなり
となる。また内部エネルギーは
である。
非直線型多原子分子の理想気体の場合
さらに、直線形状ではない多原子分子の場合、原子の形状を規定するには回転角もパラメータが3つ必要になる。それゆえ、非直線型多原子分子が理想気体的に振舞う場合は ![]() のエネルギーが3つの並進、3つの回転の自由度に分配され、定積比熱は$$C_V=\frac{dU}{dT}=(3+3) n N_A \frac12 k_B =3nR \tag{5.4.15}$$となる。
のエネルギーが3つの並進、3つの回転の自由度に分配され、定積比熱は$$C_V=\frac{dU}{dT}=(3+3) n N_A \frac12 k_B =3nR \tag{5.4.15}$$となる。
| ↑1 | 回転のエネルギーについては分配可能であるが、低温になると分配できなくなるので比熱が変わる。 |
|---|