熱力学第一法則
熱力学の第一法則はエネルギー保存則で、式としては系の内部エネルギーの変化を ΔU 、外部から系に加えられた熱をq、外部から系にされた仕事をwとして、
のように記述される。本講義では系からの物質の出入りが遮断された閉鎖系を扱うがその場合この式は、外界からのエネルギーの出入り( q+w )がない限り一定であることを意味している。
また、孤立系では外部からの熱も仕事も加わらないので$$\Delta U=0 \tag{5.2.2}$$であり、「孤立系のエネルギーの総量は変化しない」といった表現がされることもある。
ここで出てきた内部エネルギー U は、原子や分子の運動エネルギー、位置エネルギーなど、系の持っているすべてのエネルギーの和である*1現実世界の分子には並進・回転・振動・電子のエネルギーなど様々なエネルギーがあるため、絶対的な内部エネルギーの値を実験的に求めるのは困難であるので、相対的な変化しか計測できない。理想気体ではこういった内部の効果は「内部構造がない」といった仮定によりなきものにしているので、運動エネルギーだけで内部エネルギーを議論できることになる。。従ってこの式は、外部から仕事や熱が加わることで内部エネルギーが増加するということを意味するとともに、内部エネルギーが変わらない(ΔU=0)なら系になされた仕事は熱として出ていくということも意味している。
仕事
それでは、系にされる仕事、系が受け取る熱というのはどのようなものだろうか?
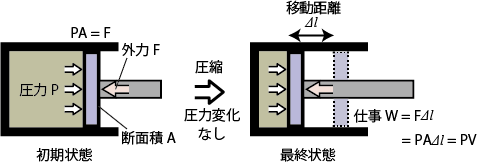
力学では、力 F が力学系に作用して距離 Δl だけ移動したとき、その力学系には FΔl の仕事がされたと考えた。下の図のように、ピストンの中に入った気体の系についても、同様に考えることができる。
たとえばピストン内部の気体を圧縮した場合、ピストンを押す力 F と移動距離 Δl の積、FΔl が気体になされた仕事である。もし、気体の圧力と等しい力をかけながら体積のみを減少させることができたならば、ピストンを押す力は F=PA となる( P は圧力、A はピストンの面積)。内部の圧力変化がないような状況なら、系になされた仕事 w は圧力×体積変化、$$w=P\Delta V \tag{5.2.3}$$ となる。
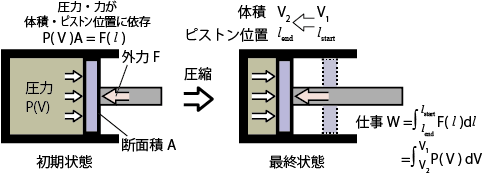
実際には体積が変わると圧力が変化するので、変化する圧力に対応するために積分を使って書く必要がある。
ピストンの位置がlstart から lend になるまで、内部圧力×ピストン面積と同じ力を外部から加えながら、非常にゆっくりと動かして体積が V1 から V2 に変化した時、系になされる仕事は、$$w=\int_{l_{end}}^{l_{start}}Fdl \tag{5.2.4}$$となる。体積 V についての積分で表すなら、これは
となる。*2各点での力のつりあいの式、PAl=Fl から ![]() として、
として、![]() の関係による置換積分、
の関係による置換積分、![]() の積分範囲の向きを変えて符号を逆転させた。
の積分範囲の向きを変えて符号を逆転させた。
最小仕事と最大仕事
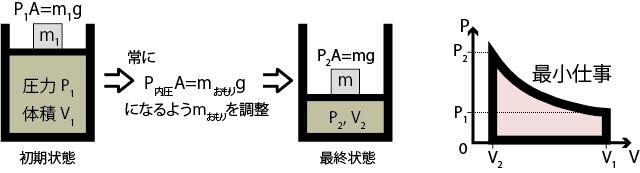
次に、さきほどの例と似ているが少し違う系として、高さ0にあるピストンの位置をピンで固定した状態で質量 m のおもりを載せた後、ピンをはずして気体の圧力により気体が圧縮するような系を考える(下図A)。ピンをはずす前の状態と圧縮後の状態で温度は変わらないとする*3温度が変わらないように外界と系の間で熱のやり取りがあると考えることにする。。この系では、圧縮の後は位置 h の点でおもりからの力と気圧による力が釣り合う状態となる。前項では外からの力と内部の気圧による力が釣り合っている状態で圧縮を行っていたが、今回はピンをはずした時点の内部の気体の圧力と外からの力は釣り合ってはいない。
今回の場合、おもりの位置エネルギー変化が外界から系になされた仕事となる。すなわち、おもりによる重力 mg と下降距離 h を掛け合わせた mgh が系になされた仕事である。また、圧縮後の圧力 P2 ×ピストン面積 A が力 mg と釣り合っているので、( mg=P2 A ) $$w=mgh=P_2 Ah=P_2 \Delta V \tag{5.2.6}$$となっているはずである( ΔV は体積変化)。
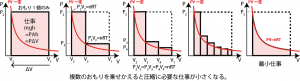
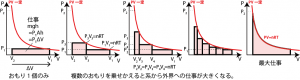
この仕事の大きさは、おもりの乗せ方を変えてやるともっと小さくすることができる。たとえば、ピストンに乗せるおもりを最初は軽いおもり(質量 m3 )を使って位置 h3まで下がって釣り合ったところで、その後質量 m のおもりに切り替えたならば、もっと小さな仕事で系を圧縮することができることになる(上図B)。最初の状況では系がなされた仕事は mgh であるが、最初軽いおもりを使った場合に系がなされた仕事は $$w=mgh–(m–m_3)gh_3 \tag{5.2.7}$$ となり、最初から質量 m のおもりが乗っているときより ![]() だけ小さくなる。
だけ小さくなる。
より多くのおもりを使用すると、系を圧縮するための仕事をより小さくすることができる。系になされた仕事はおもりの位置エネルギー変化と等しい。ピストンが下降して停止した位置では重力とピストンの圧力が釣り合った状態になっているので、釣り合いの各点における圧力と体積変化の積が位置エネルギー変化と等しくなる*4P3ΔV3=P3Ah3=m3gh3。ただしΔV3, h3は、質量m3のおもりを使って圧縮しときの体積変化とおもりの高さ変化。。また理想気体を考えるなら、おもりを交換するときの系の圧力・体積はPV一定の等温線上にある。*5圧力P3・体積V3はP3V3=nRTをみたす。
それでは、系がなされる仕事の大きさが最小になるときはどのような状況かといえば、最初の状態から最後の状態まで常におもりからの力と圧力が釣り合っているように、おもりの質量を調整しながら圧縮した場合である。理想気体ならば、この状況はPV一定の等温線上を推移させたときになる。このような状況での仕事のことを最小仕事と呼ぶ。
一方、ピストンの圧力がおもりの重力よりも大きく、おもりを乗せた後ピストンが上昇する場合、最初から質量 m のおもりを乗せた時よりも、少し重いおもりを乗せて開始したほうが系から外界への仕事は大きくなる*6極端な場合、おもりの質量が0( m =0 のとき、系にされる仕事は0である。( w =0)。また、ピストンが上昇する場合に系がされる仕事が最大になる状況は、おもりによる力と圧力が常に釣り合っているように、おもりの質量をたえず調整しながら等温線上の圧力・体積にて上昇させた場合である。このときの仕事は最大仕事と呼ばれる。
最小仕事と最大仕事は、いずれもPV図上で等温線上を経由して、常に外からの力と内部の圧力が釣り合うように、平衡状態を保ちながら圧縮、膨張させたときの仕事であり、最小仕事=最大仕事となる。このように、常に外力と内部圧力が釣り合うように、平衡状態を保ちながらゆっくりと圧縮、膨張させるような操作(準静的過程)は可逆過程と呼ばれる。
一方、当初の条件のように、おもりの質量を変えないまま圧縮を行ったような場合は内部からの圧力による力と外部から系に加わっている力が異なっている。このような条件では、系の内部で平衡状態が保たれず、非平衡状態を経由することになる。また圧縮に必要な仕事と膨張の仕事の大きさが等しくなることもない。このような過程は不可逆過程と呼ばれる。
| ↑1 | 現実世界の分子には並進・回転・振動・電子のエネルギーなど様々なエネルギーがあるため、絶対的な内部エネルギーの値を実験的に求めるのは困難であるので、相対的な変化しか計測できない。理想気体ではこういった内部の効果は「内部構造がない」といった仮定によりなきものにしているので、運動エネルギーだけで内部エネルギーを議論できることになる。 |
|---|---|
| ↑2 | 各点での力のつりあいの式、PAl=Fl から |
| ↑3 | 温度が変わらないように外界と系の間で熱のやり取りがあると考えることにする。 |
| ↑4 | P3ΔV3=P3Ah3=m3gh3。ただしΔV3, h3は、質量m3のおもりを使って圧縮しときの体積変化とおもりの高さ変化。 |
| ↑5 | 圧力P3・体積V3はP3V3=nRTをみたす。 |
| ↑6 | 極端な場合、おもりの質量が0( m =0 のとき、系にされる仕事は0である。( w =0) |