この節では理想気体の状態方程式について復習をしたい。理想気体の状態方程式は大学入試問題を解くのに散々利用してきたと思う。これらはボイルの法則、シャルルの法則と、アボガドロの法則の３つの法則を組み合わせたもので、17世紀から19世紀にかけて知られることになった法則である

ボイルの法則

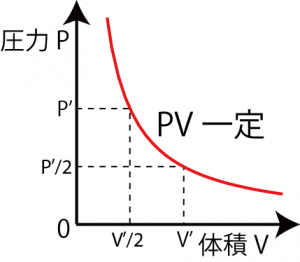
このうち最も古いものがボイルの法則で、17世紀(1662年)にイギリスのボイルによって示された法則である。この法則では気体の体積と圧力が反比例の関係にある(言い換えると体積と圧力の逆数が比例関係にある, )ことを示すものであり、式で表すと

と表すことができる。（温度・物質量一定条件にて。比例定数を k で表して。）つまり、体積×圧力が一定(PV一定)になるので、気体の体積、圧力の一方が変わった時にもう一方がどう変わるかを計算することができるようになる。

たとえば体積が2倍になったなら圧力は1/2に、圧力が10倍になったなら体積が1/10になったことがわかるわけである。

シャルルの法則と絶対零度

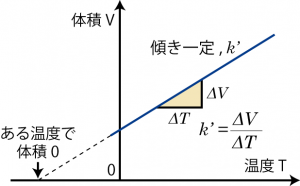
シャルルの法則は18世紀末にフランスのシャルルが発見し(1787)、ゲイリュサックにより発表(1802)された法則で、圧力一定条件で温度変化 ΔT と体積変化 ΔV の比が一定、つまり定数 k’ を使ってのように結びついていることを示すものである。

この法則は、気体の温度と体積を圧力一定条件で記録していくと１つの直線上に乗る…というところから発見されたものである。一方、体積と温度が１つの直線上に乗るならば、温度を下げていくことでそのうち体積が０になってしまう…ということも見出された。しかし、実際に体積がゼロになったり負になったりすることは考えにくいので、温度には下限があるのだろう…ということになった。この温度の下限が絶対零度と呼ばれるもので、摂氏で −273.15 ℃である。 逆にこの絶対零度を原点にとって定義した温度が絶対温度、熱力学温度であり、K （ケルビン）という単位が熱力学に従って定義されている。

絶対温度を使ってシャルルの法則を考えると気体の体積と温度は比例関係、 となり、従って比例定数( k’ )を使って

と書けることになる。シャルルの法則を使うことで、気体の体積が変化した時の温度変化を計算できるようになる。

アボガドロの法則

理想気体の状態方程式、PV = nRT を構成するもう１つの法則がアボガドロの法則である。19世紀初頭は分子と原子の区別がまだついていなかったので、原子というものがあったとしても、化学結合で分子になっているといったことは想定されていなかった。しかし、原子の数がそのまま体積と比例していると考えた場合、例えば水素 2 L と酸素 1 L から水ができるときは、水素と酸素の原子の数を合わせた ３ L になってもよいことになるが、実際には 2 L の水蒸気にしかならない。そこで原子、分子を区別して、気体の体積は分子の数に比例すると考えることにした。そうすれば上記のような食い違いは生じることはなくなる。こうして提唱された法則がアボガドロの法則、「同一圧力、同一温度、同一体積のすべての種類の気体には同じ数の分子が含まれる」というものであり、1811年にイタリアのアボガドロによって提唱された。

理想気体の状態方程式

以上、３つの法則をまとめたものが理想気体の状態方程式、

である。Rは気体定数と呼ばれる定数で、任意の体積、物質量、圧力のうち２つを決めてこの式に代入してやれば残りの１つを求めることができる。とはいえ、現実の気体は常にこの式に従うわけではない。実際の気体では分子に大きさや相互作用があるため、圧力が高い場合、温度が非常に低い場合など、ボイルの法則・シャルルの法則に従わないことも多い。そこで、この式に厳密に従う気体のことを理想気体と呼び、現実の気体（実在気体）と区別している。