ここまで見てきたように、化学結合は2個の原子の軌道が重なり合って生成した結合性の軌道に2個の電子が共有されることで生成される。しかし、原子の軌道の重なり合いは、必ずしも2個の原子とは限らない。特に、π結合はp軌道が並んで重なり合うことで生成するということから、p軌道がもっと沢山の並んだときにどうなるのか、疑問に思うこともあるかもしれない。実際、たくさんのp軌道が隣り合ってπ結合を生成した場合は、2個の炭素原子がπ結合を生成するときとは少し違う様相となる。
π共役分子:ブタジエン — 2つのπ結合が隣接
ブタジエンはタイヤなどに使われる合成ゴムの原料になる分子で、次のような構造をとる。
この分子は4個の炭素原子と6個の水素原子が同一平面内で結びついており、炭素についてはσ結合だけでなくπ結合も加わることで二重結合も形づくっている。これらπ結合は、分子がなす平面と垂直方向に伸びている2p軌道同士の重なりで生じることになる。前節まででは、2個の原子のp軌道が重なることで結合性軌道と反結合性軌道が生成していた。しかし今回のブタジエン分子については、4つのp軌道が並んでいるわけで、中央の2つの炭素原子同士(C2, C3)でも2p軌道同士が重なりを持ちそうに見えないだろうか?
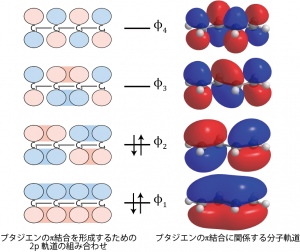
そこで次の図では、これら4つの2p軌道について符号![]() を組み合わせた軌道を作り、エネルギーの低いものから順に電子を入れていってみた。4つの原子のp軌道には4つの電子が入っていたので、実際に電子が入る軌道は
を組み合わせた軌道を作り、エネルギーの低いものから順に電子を入れていってみた。4つの原子のp軌道には4つの電子が入っていたので、実際に電子が入る軌道は![]() の2つである。したがってこれら2つの軌道が原子間の結合の性質を決めることになる。
の2つである。したがってこれら2つの軌道が原子間の結合の性質を決めることになる。
水素原子の1s軌道から結合性軌道・反結合性軌道を作った時は組み合わせは足し算したものと引き算したものの2種類だったが。今回は4つのp軌道があるので4種類の組み合わせがある。それぞれの原子核の間に電子が存在確率を持つ軌道と持たない軌道があるのがわかるだろうか?
最もエネルギーが低い軌道、![]() は4つの原子全ての間で電子が存在確率を持つ。したがってこの軌道に入った2個の電子は C1-C2、C3-C4の間だけでなく、C2-C3間にも結合を作ろうとする性質を持つことになる。一方、次の軌道、
は4つの原子全ての間で電子が存在確率を持つ。したがってこの軌道に入った2個の電子は C1-C2、C3-C4の間だけでなく、C2-C3間にも結合を作ろうとする性質を持つことになる。一方、次の軌道、![]() では、C1-C2、C3-C4間は
では、C1-C2、C3-C4間は![]() と同様、結合性の性質を持つのに対し、C2, C3の間では符号が変わってしまい、電子が存在しない状態になる。つまり反結合性軌道の性質を持つ。結局、C1-C2、C3-C4間については2つの軌道のどちらもが結合性の性質を持っているためにπ結合を生成しているのに対し、C2, C3の間にはπ結合が生成しないということになる。
と同様、結合性の性質を持つのに対し、C2, C3の間では符号が変わってしまい、電子が存在しない状態になる。つまり反結合性軌道の性質を持つ。結局、C1-C2、C3-C4間については2つの軌道のどちらもが結合性の性質を持っているためにπ結合を生成しているのに対し、C2, C3の間にはπ結合が生成しないということになる。
とはいえ、![]() であった軌道の重なりによる影響がないわけではない。ブタジエンの中央のC-C結合は 1.47 Å (0.147 nm) となっており、通常の飽和炭化水素のC-C単結合の値、1.54 Å (0.154 nm)と比べて少し短い。このようにπ結合が並んで相互作用することで、分子全体として安定化されているような分子はπ共役分子と呼ばれる。
であった軌道の重なりによる影響がないわけではない。ブタジエンの中央のC-C結合は 1.47 Å (0.147 nm) となっており、通常の飽和炭化水素のC-C単結合の値、1.54 Å (0.154 nm)と比べて少し短い。このようにπ結合が並んで相互作用することで、分子全体として安定化されているような分子はπ共役分子と呼ばれる。
- ブタジエンのC-C:1.47Å, C=C:1.37Å
- エチレンのC=C:1.34Å
- 飽和炭化水素のC-C:1.54Å
π共役分子:ベンゼン — 等価な6つのp軌道
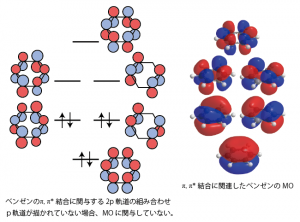
代表的なπ共役分子としてはベンゼンがある。ベンゼンでは、等価な6つのp軌道が環状に並んでいるため、π結合が関与する分子軌道は6つのp軌道の符号の組み合わせから次の図のようになる。このような電子状態になると、分子全体のエネルギーがより低く安定になるため、ベンゼン環を構成するπ結合は、通常のπ結合と比べて反応しにくい。
また、電子が入っている軌道について見てみると、エネルギーがもっとも低い軌道は6つの炭素原子すべてで符号が同じになっており、すぺてのCC結合間にπ結合性の2p軌道同士の重なりがあることがわかる。また、よりエネルギーが高い2つの軌道についても、隣り合う炭素同士の2p軌道の重なりがどちらかの軌道に必ず存在している。実際に、ベンゼンのCC結合間距離はどの炭素間でも同じになっており、各々の炭素は同じ性質を持っていると考えられている。
固体の電子状態のLCAO的イメージ
2個以上の原子軌道による軌道の重なりは結晶の場合にはより顕著になる。たとえば、リチウム原子が一列に並んだようなものを考えてみることにしよう。リチウム原子では、1s軌道に2個の電子が、2s軌道に1個の電子が入っているので、隣の原子の2s軌道の電子を共有することで結合ができると考えることにしよう。しかし、今回もブタジエンの時と同様、原子の両隣に2s軌道が存在する。そこで、これらたくさんの原子の軌道についても、符号を組み合わせてエネルギーの低いものから高いものへ、下から上に順に並べてみたのが次の図である。
一番下の列から、符号が全く同じ場合、途中で符号が変わる場合、そして一番上は原子1個おきに符号が反転している場合である。電子はエネルギーが最も低い状態(すべて符号が同じ状態)から順に詰まっていく。原子の数が多いほど、こうしてできた多数の軌道のエネルギーの間隔は小さくなり、連続的になっていく。このような軌道のまとまりはバンドと呼ばれる。
このように、固体においては多数の軌道をまとめてバンドとして扱う場合が多い。
金属と半導体・絶縁体
ここで、バンドのでき方にはいくつかの種類がある。上で出てきたリチウムの場合、もともと2s軌道には1個の電子しか入っていなかったので、2s軌道でできた連続的なバンドの真ん中までしか電子が入っていない。このような物質では、少しエネルギーが加わることで電子が入っていない軌道(空軌道)に電子を簡単に励起することができるので、熱的なエネルギー*1分子や原子はそれらが置かれた温度に応じた運動のエネルギーを持っており、エネルギーのやりとりも起きている。である程度の数の電子が空軌道に存在するようになる。こうして励起された電子は、存在確率が異なる別の空軌道にも移ることができるわけなので、一見、金属内を電子が自由に運動しているように見えるようになる。このような物質が金属であり、電気伝導性を持つ。また励起された電子は自由電子と呼ばれる。
一方、金属以外の半導体や絶縁体といった物質では、バンドを構成する全ての軌道に電子が詰まっていることがある。このような場合、電子が詰まっているバンド(価電子帯)と電子が詰まっていないバンド(伝導帯)の間にはエネルギー差がある。これはバンドギャップと呼ばれ、電子はバンドギャップを超える大きなエネルギーをもらって他のバンドに移動しなければ動き回ることができない。半導体ではバンドギャップは小さく、絶縁体では大きい。金属にはバンドギャップが存在しない。これが電気伝導性に影響している。
絶縁体の例として塩化ナトリウムを考えてみる。塩化ナトリウムでは、もともとナトリウムの3s軌道に入っていた1個の電子が塩素の3p軌道に入ってしまい、そのためにナトリウムが陽イオンに、塩素が陰イオンになってイオン結晶を作っている。これをバンドとして考えるならば、塩素の3p軌道でできたバンド:価電子帯とナトリウムの3s軌道からなるバンド:伝導帯があって、塩素の3p軌道由来の価電子帯には電子が詰まっていて、ナトリウムの3s軌道由来の伝導帯には電子が入っていないと考えることになる。そして、価電子帯には電子が詰まっているのでバンド内部に空軌道はない。つまり、伝導帯から価電子帯に電子が励起されない限り、自由電子は生じないことになる。そして、これら2つのバンドはエネルギーが大きく異なり、バンドギャップが非常に大きい。それゆえ塩化ナトリウムには電気伝導性がないことになる。
半導体の場合も絶縁体の場合と同じようにバンドギャップが存在する。ただ、半導体の場合はバンドギャップのエネルギーが小さいので、熱的なエネルギーでも下のバンド(価電子帯)から上のバンド(伝導帯)に電子を励起することができる。その結果、ある程度の数の電子が伝導帯に存在することになるので、金属ほどではないものの、電気伝導性を持つことになる。
| ↑1 | 分子や原子はそれらが置かれた温度に応じた運動のエネルギーを持っており、エネルギーのやりとりも起きている。 |
|---|