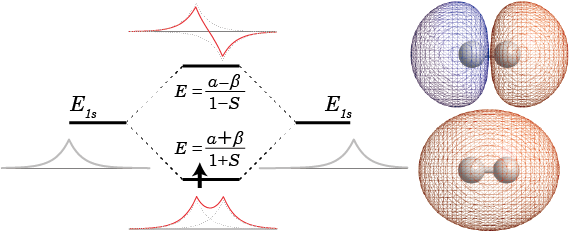
それでは実際に、分子のハミルトニアンと波動関数についての例を見ていくことにしよう。まずは最も単純な例として、電子が1個の水素分子イオンを考える。水素分子ではなくわざわざ水素分子”イオン”なのは、電子2個以上だと解けないシュレディンガー方程式が、電子が1個の場合解けるためである。

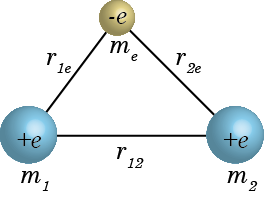
まずは上図のような、質量 m₁, m₂ の原子核と m_e の原子核が距離 r₁₂, r_1e, r_2e で結びついている水素分子イオンのハミルトニアンを完全な形で書いてみると、$$\hat H_{H_2^+}=\underbrace{-\frac{h^2}{8\pi m_e}\nabla_e^2-\frac{e^2}{4\pi\varepsilon_0}\left(\frac{1}{r_{1e}}+\frac{1}{r_{2e}}\right)}_{この部分を電子についてのハミルトニアン\hat Hとする}\underbrace{-\frac{h^2}{8\pi m_1}\nabla_1^2-\frac{h^2}{8\pi m_2}\nabla_2^2+\frac{e^2}{4\pi\varepsilon_0}\frac{1}{r_{12}}}_{こちらは核についての式なので分離}\tag{2.4.1}$$のようになる。

原子のときと同様、 は運動エネルギーを のように考えて運動量mvを 等に置き換えたものであり、 は電場による位置エネルギー（ポテンシャルエネルギー）に対応している。また、式の前半分が電子について、後ろ半分が原子核についてのの式となっている。

前節で述べたように、ここから振動や回転、並進といった核の運動にあたる式後半部分を取り除いて、電子の成分のみを分けて考えたときの式、$$E\Psi=\hat H\Psi\tag{2.4.2}$$が、水素分子イオンの電子についての時間に依存しないシュレディンガー方程式である^*1。

この式の波動関数として、先に述べたLCAO近似に基づき、水素原子2個の波動関数の組み合わせ、$$\Psi=c_1\phi_1+c_2\phi_2\tag{2.4.3}$$を解として想定する。ここで、波動関数について、その大きさの2乗が確率であることと、全ての空間での存在確率の足し合わせが1である（水素分子イオンでは空間内のどこかには電子が必ず存在する）ことを利用して、また を全空間における積分を意味することにすると、$$\int\Psi^2 d\tau=1\tag{2.4.4}$$になるはずである。従って、$$1=\int\Psi^2 d\tau=c_1^2 \int\phi_1^2 d\tau+c_2^2 \int\phi_2^2 d\tau+2c_1 c_2 \int\phi_1 \phi_2 d\tau\tag{2.4.5}$$となる。なお、原子の波動関数についても全空間で積分すると１になったので$$\int\phi_1^2 d\tau=1, \int\phi_2^2 d\tau=1\tag{2.4.6}$$である。
ここで、唯一１とならない重なり積分を記号Sを使って$$S=\int\phi_1\phi_2 d\tau\tag{2.4.7}$$と書くと、この式は結局$$1=c_1^2+c_2^2+2c_1 c_2 S \tag{2.4.8}$$ と書き表すことができる。

結合性軌道と反結合性軌道

さて、水素原子には、量子数に応じて様々な解（1s, 2s, 2p…）が存在した。今回考えている水素分子イオンについて電子が入る軌道を考える際、エネルギーが最も低い状態は水素原子の１ｓ軌道の組み合わせであると考えるのは自然なことだと思われる。そこで、もっとも単純な系としてが各原子の1s軌道の波動関数であったときのことを考えてみる。2つの原子核は同じ電荷を持ち、定常状態ではどちらかが特別ということもない。従って電子についても2個の原子核に同じ確率で属すると考えることができるので、 の中では $$c_1^2=c_2^2\tag{2.4.9}$$ となっていると考えるのも自然だろう。
こうすると、になり、 に代入すると$$c_1=\frac{1}{\sqrt{1\pm S}}\tag{2.4.10}$$となる。
ここまでくると、実際の波動関数の形を描くことができる。

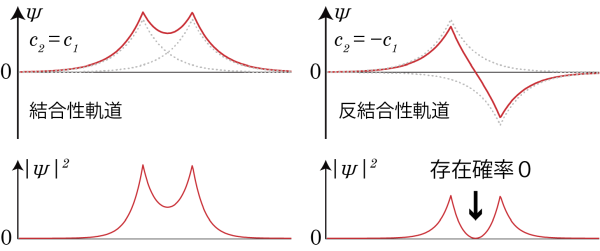
図のように、 の場合の波動関数は２つの原子間の波動関数の値は重ね合わされて大きくなるのに対して、 の場合の波動関数では、２つの原子軌道間で符号が逆転しているために原子の間で電子の存在確率が０になる場所が存在することになる。これらを結合性軌道、反結合性軌道と呼ぶ。電子が結合性軌道にあるときは水素分子イオンは結合を作るが、反結合性軌道に電子が存在する場合は水素分子イオンは安定に存在できず、2個の原子核は離れていってしまう^*2これを少し見方を変え、クーロン力による古典的な説明をしてみよう。
結合性軌道に電子がいるとき、波動関数の振幅は原子核の間で大きく、したがって電子は原子核の間に存在する確率が高い。それゆえ、原子間の電子は２つの電子核をクーロン力で引き止めることができ、したがって結合が生成する。一方、反結合性軌道に電子がある場合は原子核の間に電子が存在する確率が低い。それゆえ、２つの原子核はクーロン力で反発するだけとなり、結合を形成することができない。。

水素分子イオンのエネルギー

次に、エネルギーについて考える。もともとのシュレディンガー方程式 の左から、の共役複素量、を掛けるととなる。Eはエネルギーであるので左に出すことができるのに対してHはハミルトニアンで、中に微分係数が入っていて右側のψを微分しなければならないので動かすことができない。従って とも書くことができる。
これを全空間で積分すると$$E\int\Psi^*\Psi d\tau=\int\Psi^*\hat H ̂\Psi d\tau\tag{2.4.11}$$となり、の関係から$$E=\int\Psi^* \hat H\Psi d\tau\tag{2.4.12}$$が得られる。これに先に求めたを入れてまとめて、同じ原子の軌道同士の積分をα、異なる原子の軌道同士の積分をβで置き換えていくと$$ E=\int\left(\frac{1}{\sqrt{1\pm S}}(\phi^*_{1s1} \pm \phi^*_{1s2})\right)\hat H\left(\frac{1}{\sqrt{1\pm S}}(\phi_{1s1}\pm \phi_{1s2})\right)d\tau $$ $$ E=\frac{1}{2(1\pm S)}\left(\underbrace{\int\phi^*_{1s1}\hat H\phi_{1s1}d\tau}_{\alpha} +\underbrace{\int\phi^*_{1s2}\hat H\phi_{1s2}d\tau}_{\alpha} \pm \underbrace{\int\phi^*_{1s1}\hat H\phi_{1s2}d\tau}_{\beta} \pm \underbrace{\int\phi^*_{1s2}\hat H\phi_{1s1}d\tau}_{\beta} \right) $$ $$ E=\frac{\alpha\pm\beta}{1±S}\tag{2.4.13}$$ となる^*3 を水素原子１について、を水素原子２についての１ｓ軌道の波動関数とする。。これらが水素分子イオンの結合性・反結合性軌道のエネルギーであり、が結合性軌道のエネルギー。が反結合性軌道のエネルギーに対応している。

ところで、これらのエネルギーを出すときに使ったハミルトニアンは水素分子イオンの電子についてのものであった。したがって、得られたエネルギーについても水素分子イオンの中の電子のエネルギーということになる。出てきたエネルギーを水素原子のエネルギーと比較してみると下の図のようになる。エネルギーの順番としては、反結合性軌道に電子が存在するときのエネルギー()よりも水素原子内に電子が存在するときのエネルギー(E_1s)のほうが小さく、さらにそれよりも結合性軌道に電子が存在するときのエネルギー()が小さいという順番になっている。

これは言い換えれば、原子の状態の水素原子で1個の陽子の周りに電子が1個存在している状態のエネルギーよりも、2個の陽子の周りに電子が1個存在して分子の波動関数が結合性軌道の形になっている状態のほうが電子のエネルギーが低く安定ということである。それゆえ、水素分子イオンは水素原子よりも安定で、水素原子と陽子が乖離せずに存在することができる。水素分子イオンは反応性が高いため通常は見られないが、分子密度がきわめて低い宇宙空間などでは観測されているのだそうだ。