高校物理で物体の動きを考えたときは、
- 力が加わっていないときどうなっているかを示すために慣性の法則があり、(第1法則)
- ニュートン運動方程式、F=maから物体に掛かる力と加速度の関係を出し、(第2法則)
- 物体間の力の掛かり方として作用・反作用の法則があって、(第3法則)
これらニュートンの運動の法則から位置や速度を計算することができた。
しかしもともとは、これら3つの法則は仮説であった。これらの3つの法則を仮説として採用して計算を行うと、得られた位置や速度など、実験で得られた現実の値を再現する。そこで、様々な物理現象を説明するときにこれら3つの法則を基本原理にすればうまくいくのではないか?…と考えてやってみたらうまくいって発展してきたのが古典力学ということになる。
ところが、原子や分子の振る舞いを考える場合は、量子論にもとづいて粒子としてだけでなく波としての振る舞いも重要となってくるので古典力学が使えなくなってしまった。そこでこの世界を説明するために現在使われているのが量子力学である。量子力学もまた、いくつかの原理に基づいて、自然現象がうまく説明できるように組み立てられている。量子力学にもいくつかの表記法があるが、ここでは代表的な原理の紹介から量子力学的世界に馴染んでいくことにする。とにかく、次に出てきたいくつかの原則(仮説)に基づいて計算していくと、古典論では説明できなかった分子や原子の振る舞いがうまく説明でき、測定結果と合致するのである。ゆえに、我々の身の回りの現象を説明するのにニュートンの3つの法則が有効な理論であるのと同じように、量子力学は原子や分子のスケールに至るまで有効な理論ということになる。
量子力学で計算を行っていくための基本的な原則(仮説)の主なものは概ね以下のようなものになる*1このように量子力学を仮説から導入している教科書としては「新物理化学(坪村宏)」、「マッカーリ・サイモン物理化学」、「量子化学(原田義也)」あたりが参考になるので、ちゃんと勉強したい場合はそちらを参照のこと。Web上だと「量子力学の基本法則」、「学部学生のための量子化学講義ノート」あたりのページも参考になるかもしれない。。
1.系の状態は波動関数 ψ(x,y,z,t) によって決められ、
波動関数の絶対値の二乗はその位置における存在確率に比例する。
量子力学では何か物体(粒子)について考える時も、個々の位置を考える代わりに存在確率を使って考えることになる。そのために使われるものが波動関数 ψ *2読み方はプサイである。この波動関数は関数という名前のとおり時間と位置の関数で、しかも値が複素数となるような複素関数である。また、波と同様に重ね合わせの原理も成り立つが、現実世界に対応する特定の物理量が存在するわけではない。
ただ、波動関数絶対値の二乗 |ψ|2 については、物体のある位置における存在確率に比例するという性質を持つ。たとえばある時間 t に粒子の位置 (x,y,z) における波動関数がψ(x,y,z,t)だったならば、その二乗 |ψ(x,y,z,t)|2 が粒子の位置 (x,y,z) における存在確率となる。*3複数の物体があるなら、波動関数の二乗は各々の物体が各々ある位置をとるときの確率となる。たとえば2個の粒子があったとして、それぞれの座標が(x1,y1,z1),(x2,y2,z2)にあるような状況は2個の粒子の6つの座標を変数とする波動関数ψ(x1,y1,z1,x2,y2,z2)の二乗、|ψ(x1,y1,z1,x2,y2,z2)|2 で表されることになる。
さらに、波動関数は存在確率に比例しているということから、ある粒子についての波動関数の絶対値の二乗は全ての空間で積分すると1になるように通常は規格化されている。これは![]() を全空間での積分を意味することにすると$$\int\left|\psi\right|^2d\tau=1\tag{1.4.1}$$というふうに書ける。この式は、空間の全てを探せば粒子は必ずどこかに、100%の確率、つまり確率1で存在するはずであることを意味している*4もし空間内に粒子が存在しないような条件があれば100%じゃないのでは?…と思う方がひょっとするといるかもしれない。しかし、ここでは「ある粒子」の運動について、粒子が存在する場合のことを考えているわけなので、粒子がどこにも存在しない場合というのは考える必要がない。それに、粒子が存在しないのなら運動について考える必要もないだろう。。
を全空間での積分を意味することにすると$$\int\left|\psi\right|^2d\tau=1\tag{1.4.1}$$というふうに書ける。この式は、空間の全てを探せば粒子は必ずどこかに、100%の確率、つまり確率1で存在するはずであることを意味している*4もし空間内に粒子が存在しないような条件があれば100%じゃないのでは?…と思う方がひょっとするといるかもしれない。しかし、ここでは「ある粒子」の運動について、粒子が存在する場合のことを考えているわけなので、粒子がどこにも存在しない場合というのは考える必要がない。それに、粒子が存在しないのなら運動について考える必要もないだろう。。
…というわけで、波動関数がわかれば物体の状態がわかるということである。
参考:波動関数の絶対値の二乗の全空間での積分を x, y, z を使って表すと…
波動関数の絶対値の二乗の全空間での積分が1に規格化されているというのは、もし粒子の位置が座標 x だけで決められるような場合なら1次元だけ考えればよいので$$\int_{-\infty}^\infty\left|\psi(x,t)\right|^2dx=1\tag{1.4.2}$$ということだ。3次元空間で考えるなら$$\int_{-\infty}^\infty\int_{-\infty}^\infty\int_{-\infty}^\infty\left|\psi(x,y,z,t)\right|^2dxdydz=1\tag{1.4.3}$$となる。ちなみに$$\int_{-\infty}^\infty\int_{-\infty}^\infty\int_{-\infty}^\infty\left|\psi(x,y,z,t)\right|^2dxdydz=\int_{-\infty}^\infty\left(\int_{-\infty}^\infty\left(\int_{-\infty}^\infty\left|\psi(x,y,z,t)\right|^2dx\right)dy \right)dz\tag{1.4.4}$$である。いずれも、各座標軸について +∞ から -∞ まで積分(つまり全ての空間で積分)すれば、必ず粒子が見つかることから積分結果は100%、すなわち1となる。
ところで複素数a+ibの絶対値の二乗は |a+ib|2=(a+ib)(a–ib) = a2+b2と表され、虚数部分の符号を反転させたa-ibはa+ibの複素共役と呼ばれる。
波動関数 ![]() も複素数なので、複素共役な関数が存在する。通常、
も複素数なので、複素共役な関数が存在する。通常、 ![]() に対応する複素共役な関数は
に対応する複素共役な関数は ![]() のように * をつけて表わされる。従って絶対値の二乗は
のように * をつけて表わされる。従って絶対値の二乗は![]() と
と![]() を掛け合わせて全空間で積分した量$$\begin{align}\int_{-\infty}^\infty\int_{-\infty}^\infty\int_{-\infty}^\infty\psi^*(x,y,z,t)\psi(x,y,z,t)dxdydz&=\int_{-\infty}^\infty\int_{-\infty}^\infty\int_{-\infty}^\infty\left|\psi(x,y,z,t)\right|^2dxdydz=1\tag{1.4.5} \\ \int_{-\infty}^\infty\psi^*(x,t)\psi(x,t)dx&=\int_{-\infty}^\infty\left|\psi(x,t)\right|^2dx=1\tag{1.4.6} \\ \int\psi^*\psi d\tau&=\int\left|\psi\right|^2 d\tau=1\tag{1.4.7}\end{align}$$ といったふうに書くこともできる
を掛け合わせて全空間で積分した量$$\begin{align}\int_{-\infty}^\infty\int_{-\infty}^\infty\int_{-\infty}^\infty\psi^*(x,y,z,t)\psi(x,y,z,t)dxdydz&=\int_{-\infty}^\infty\int_{-\infty}^\infty\int_{-\infty}^\infty\left|\psi(x,y,z,t)\right|^2dxdydz=1\tag{1.4.5} \\ \int_{-\infty}^\infty\psi^*(x,t)\psi(x,t)dx&=\int_{-\infty}^\infty\left|\psi(x,t)\right|^2dx=1\tag{1.4.6} \\ \int\psi^*\psi d\tau&=\int\left|\psi\right|^2 d\tau=1\tag{1.4.7}\end{align}$$ といったふうに書くこともできる
2.波動関数 ψ は時間に依存するシュレディンガー方程式をみたす。
波動関数が満たす方程式が前節(1.3.23)でも出てきた時間に依存するシュレディンガー方程式(シュレディンガー方程式と略すことも)$$\frac{ih}{2\pi}\frac\partial{\partial t}\psi(x_1,y_1,z_1,…,t)=\hat H\psi(x_1,y_1,z_1,…,t)\tag{1.4.8}$$である*5一般には座標は粒子1個とは限らないので、波動関数は系を構成する粒子の個数分の座標の関数ということになるので(x1,y1,z1,…)と表記した。。右辺の![]() はハミルトン演算子(ハミルトニアン)とも呼ばれる量で、古典力学の運動エネルギーと位置エネルギー(ポテンシャルエネルギー)を足し合わせた量の中の運動量 p に対応する項を
はハミルトン演算子(ハミルトニアン)とも呼ばれる量で、古典力学の運動エネルギーと位置エネルギー(ポテンシャルエネルギー)を足し合わせた量の中の運動量 p に対応する項を ![]() に置き換えて作ったものである。
に置き換えて作ったものである。![]() の中にも ψ を偏微分する
の中にも ψ を偏微分する![]() が入っているので、結局ハミルトン演算子は左辺・右辺で波動関数を時間・位置で微分するようなものになっている。微分は順番を入れ替えることができないし、関数 ψ を微分したら別の関数になってしまうので、シュレディンガー方程式では両辺にψがあるからといってそのままψを消してしまうようなことはできない。
が入っているので、結局ハミルトン演算子は左辺・右辺で波動関数を時間・位置で微分するようなものになっている。微分は順番を入れ替えることができないし、関数 ψ を微分したら別の関数になってしまうので、シュレディンガー方程式では両辺にψがあるからといってそのままψを消してしまうようなことはできない。
参考:時間に依存するシュレディンガー方程式の例(1次元版)いろいろ
はじめに、粒子が1個あって何も力を受けていない時のシュレディンガー方程式を考えてみる。シュレディンガー方程式におけるハミルトニアン![]() は古典力学の運動エネルギーと位置エネルギー(ポテンシャルエネルギー)を足し合わせた量から作る。簡単のために1次元(座標 x )のときを考え、質量 m 、速度 v の粒子が1個があったとする。このとき、全エネルギーは
は古典力学の運動エネルギーと位置エネルギー(ポテンシャルエネルギー)を足し合わせた量から作る。簡単のために1次元(座標 x )のときを考え、質量 m 、速度 v の粒子が1個があったとする。このとき、全エネルギーは ![]() である。これを運動量 p=mv を使って表すと、
である。これを運動量 p=mv を使って表すと、![]() である。そこで、この p を
である。そこで、この p を![]() に置き換えて作ったハミルトニアンを使って作った$$\frac{ih}{2\pi}\frac\partial{\partial t}\psi(x,t)=-\frac{h^2}{8\pi^2m}\frac{\partial^2}{\partial x^2}\psi(x,t)\tag{1.4.9}$$が粒子1個が運動している場合のシュレディンガー方程式となる。
に置き換えて作ったハミルトニアンを使って作った$$\frac{ih}{2\pi}\frac\partial{\partial t}\psi(x,t)=-\frac{h^2}{8\pi^2m}\frac{\partial^2}{\partial x^2}\psi(x,t)\tag{1.4.9}$$が粒子1個が運動している場合のシュレディンガー方程式となる。
もし、この粒子が何らかの磁場や電場、重力などから力を受けていたならば、粒子は位置に応じて位置エネルギー V(x) も持っているはずなので、シュレディンガー方程式は$$\frac{ih}{2\pi}\frac\partial{\partial t}\psi(x,t)=\left[-\frac{h^2}{8\pi^2m}\frac{\partial^2}{\partial x^2}+V(x)\right]\psi(x,t)\tag{1.4.10}$$となる。
一方、お互い力を及ぼさない粒子2個(座標 x1, x2 )が運動している場合を考える。このときそれぞれの粒子の質量が m1, m2、それぞれの位置エネルギーが V1(x1), V2(x2) だったとする。このとき、シュレディンガー方程式は$$\frac{ih}{2\pi}\frac\partial{\partial t}\psi(x_1,x_2)=\left[-\frac{h^2}{8\pi^2m_1}\frac{\partial^2}{\partial x_1^2}-\frac{h^2}{8\pi^2m_2}\frac{\partial^2}{\partial x_2^2}+V_1(x_1)+V_2(x_2)\right]\psi(x_1,x_2,t)\tag{1.4.11}$$となる。
3.時刻 t において座標 x ・運動量 p で決まるような物理量 F に対しても、運動量 p を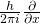 に置き換えて作る演算子
に置き換えて作る演算子 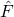 というものを考える。
というものを考える。
前項でシュレディンガー方程式を出す時は全エネルギーに対応する式の中の運動量 p の部分を![]() と入れ替えたが、ほかの物理量についても、その物理量を運動量と位置を使って書いた時の式の運動量を
と入れ替えたが、ほかの物理量についても、その物理量を運動量と位置を使って書いた時の式の運動量を![]() と入れ替えた演算子を考えることで、その物理量の値の計算を行うことができるようになる。
と入れ替えた演算子を考えることで、その物理量の値の計算を行うことができるようになる。
参考:いろいろな演算子の例
例として、ある方向の運動量や速度、運動エネルギーがどのような演算子になるかを示してみよう。
はじめに x方向の運動量 p について考えてみる。この場合、運動量の演算子は上記で述べたとおり$$\hat p=\frac{h}{2\pi i}\frac{\partial}{\partial x}\tag{1.4.12}$$となる。次に、速度 v について考えてみる。速度は運動量を使って表すと![]() と書くことができる。そこで、この中の p を
と書くことができる。そこで、この中の p を![]() に置き換えたもの、$$\hat v=\frac{h}{2\pi im}\frac{\partial}{\partial x}\tag{1.4.13}$$ が速度の演算子となる。運動エネルギー
に置き換えたもの、$$\hat v=\frac{h}{2\pi im}\frac{\partial}{\partial x}\tag{1.4.13}$$ が速度の演算子となる。運動エネルギー ![]() の場合も同様だ。やはりpを置き換えることで得られる$$\hat E=\left(\frac{h}{2\pi i}\frac{\partial}{\partial x}\right)^2\frac{1}{2m}=-\frac{h^2}{8\pi^2 m}\frac{\partial^2}{\partial x^2}\tag{1.4.14}$$が運動エネルギーの演算子となる。時間に依存するシュレディンガー方程式を作るときにも使ったものだ。
の場合も同様だ。やはりpを置き換えることで得られる$$\hat E=\left(\frac{h}{2\pi i}\frac{\partial}{\partial x}\right)^2\frac{1}{2m}=-\frac{h^2}{8\pi^2 m}\frac{\partial^2}{\partial x^2}\tag{1.4.14}$$が運動エネルギーの演算子となる。時間に依存するシュレディンガー方程式を作るときにも使ったものだ。
一方、位置 x を知りたい時はどうだろうか。位置を運動量を使って表すことはできない。従って置き換えをする必要もない。そんなわけで、位置の演算子は$$\hat x=x\tag{1.4.15}$$となる。
なお、こうして作った量子力学の演算子は、区別のために^や~の記号をつけて![]() や
や![]() と書くことが多い。
と書くことが多い。
4.物理量 F を観測したときの値は 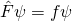 を解くことで得られる。
を解くことで得られる。
実際に物理量を計算するときは、系の状態をシュレディンガー方程式から求めて、その波動関数と物理量の演算子に関する上式を解くことで得られる。
参考:演算子と波動関数から測定値(の期待値)を求める例
前項の例なら、各々の演算子に波動関数を掛けたものの計算をおこなうことになるので、
運動量なら$$\frac{h}{2\pi i}\frac{\partial}{\partial x}\psi=f\psi\tag{1.4.16}$$速度なら$$\frac{h}{2\pi im}\frac{\partial}{\partial x}\psi=f\psi\tag{1.4.17}$$運動エネルギーなら$$-\frac{h^2}{8\pi^2 m}\frac{\partial^2}{\partial x^2}\psi=f\psi\tag{1.4.18}$$を満たすような値 f を求めれば各々の物理量の観測値がわかるということになる。
とはいえ、各々の演算子には微分の演算子![]() が入っているので、実際には波動関数がどんな関数であるかを求めた上で、実際に偏微分して…といった計算を行わないと f の値は分からない。
が入っているので、実際には波動関数がどんな関数であるかを求めた上で、実際に偏微分して…といった計算を行わないと f の値は分からない。
参考:f の値を求める計算
それでは波動関数 ψ の形が分かっているところから![]() の f の値を求めるにはどうすればよいだろうか。
の f の値を求めるにはどうすればよいだろうか。
まずは、![]() に左から波動関数の複素共役、
に左から波動関数の複素共役、![]() を掛けて積分してみよう。$$\int_{-\infty}^\infty\psi^*(x,t)\hat F\psi(x,t)dx=\int_{-\infty}^\infty\psi^*(x,t)f\psi(x,t)dx\tag{1.4.19}$$ $$\int_{-\infty}^\infty\psi^*(x,t)\hat F\psi(x,t)dx=f\int_{-\infty}^\infty\psi^*(x,t)\psi(x,t)dx\tag{1.4.20}$$ 右辺の f はただの数で、x についての積分とは関係ないので積分の外に出すことができる*6左辺では
を掛けて積分してみよう。$$\int_{-\infty}^\infty\psi^*(x,t)\hat F\psi(x,t)dx=\int_{-\infty}^\infty\psi^*(x,t)f\psi(x,t)dx\tag{1.4.19}$$ $$\int_{-\infty}^\infty\psi^*(x,t)\hat F\psi(x,t)dx=f\int_{-\infty}^\infty\psi^*(x,t)\psi(x,t)dx\tag{1.4.20}$$ 右辺の f はただの数で、x についての積分とは関係ないので積分の外に出すことができる*6左辺では![]() 内でψを微分する処理も含めてxの関数になっているので
内でψを微分する処理も含めてxの関数になっているので![]() を積分の外に出すことはできない。。(1.4.6)で示したように
を積分の外に出すことはできない。。(1.4.6)で示したように![]() なので、結局右辺は$$\int_{-\infty}^\infty\psi^*(x,t)\hat F\psi(x,t)dx=f\tag{1.4.21}$$という計算をすれば f の値が分かるということになる。
なので、結局右辺は$$\int_{-\infty}^\infty\psi^*(x,t)\hat F\psi(x,t)dx=f\tag{1.4.21}$$という計算をすれば f の値が分かるということになる。
参考:位置と運動量の交換関係
波動関数の形にかかわらず一定の値が出てくるような演算子もある。F=xp-pxという量を考えてみる。この量の演算子は![]() となる。そこで
となる。そこで![]() を考えると$$\left(x\frac{h}{2\pi i}\frac{\partial}{\partial x}-\frac{h}{2\pi i}\frac{\partial}{\partial x}x\right)\psi=f\psi\tag{1.4.22}$$となる。実際に左辺を計算してみると、$$左辺=x\frac{h}{2\pi i}\frac{\partial}{\partial x}\psi-\frac{h}{2\pi i}\frac{\partial}{\partial x}x\psi=x\frac{h}{2\pi i}\frac{\partial}{\partial x}\psi-\frac{h}{2\pi i}\psi-x\frac{h}{2\pi i}\frac{\partial}{\partial x}\psi=-\frac{ih}{2\pi ii}=\frac{ih}{2\pi}\psi\tag{1.4.23}$$となる。(途中、微分公式 (fg)’ = f‘g + fg‘ を使った。)
を考えると$$\left(x\frac{h}{2\pi i}\frac{\partial}{\partial x}-\frac{h}{2\pi i}\frac{\partial}{\partial x}x\right)\psi=f\psi\tag{1.4.22}$$となる。実際に左辺を計算してみると、$$左辺=x\frac{h}{2\pi i}\frac{\partial}{\partial x}\psi-\frac{h}{2\pi i}\frac{\partial}{\partial x}x\psi=x\frac{h}{2\pi i}\frac{\partial}{\partial x}\psi-\frac{h}{2\pi i}\psi-x\frac{h}{2\pi i}\frac{\partial}{\partial x}\psi=-\frac{ih}{2\pi ii}=\frac{ih}{2\pi}\psi\tag{1.4.23}$$となる。(途中、微分公式 (fg)’ = f‘g + fg‘ を使った。)
結果として![]() となるため、
となるため、![]() ということになる。
ということになる。
またこの計算は$$\hat x\hat p-\hat p\hat x=\frac{ih}{2\pi}\tag{1.4.24}$$という対応関係も意味している。
古典力学ではxp-pxという値は常にゼロ(xp-px=0)となり、位置xと運動量pの交換法則(xp=px)が常に成り立っていたものが、量子力学ではこの量がゼロになることはなく、従って演算子の交換法則は成り立たず(![]() )、しかも
)、しかも![]() という非常に小さな値をとることがわかる。
という非常に小さな値をとることがわかる。
これは、古典物理の力学で扱ってきた世界では 1.05i×10-34 という値は小さすぎて無視できる量だったから xp-px=0 と考えても特に支障がなかったものが、量子力学で電子や原子といった小さな粒子を扱うようになると、この小さな量が無視できない大きさになってしまう!…といったイメージで捉えることもできるかもしれない。
以上のとおり、量子力学といえども古典力学と全く関連性がない理論体系というわけではなく、古典力学で出てくる物理量を見方を変えて組み替えた理論であると捉えることもできる。古典力学では確固たる量として表されていた位置や運動量を、波動関数と位置演算子x、運動量の演算子を使って確率として扱う形に拡張していると考えるのも1つのイメージかもしれない。
| ↑1 | このように量子力学を仮説から導入している教科書としては「新物理化学(坪村宏)」、「マッカーリ・サイモン物理化学」、「量子化学(原田義也)」あたりが参考になるので、ちゃんと勉強したい場合はそちらを参照のこと。Web上だと「量子力学の基本法則」、「学部学生のための量子化学講義ノート」あたりのページも参考になるかもしれない。 |
|---|---|
| ↑2 | 読み方はプサイ |
| ↑3 | 複数の物体があるなら、波動関数の二乗は各々の物体が各々ある位置をとるときの確率となる。たとえば2個の粒子があったとして、それぞれの座標が(x1,y1,z1),(x2,y2,z2)にあるような状況は2個の粒子の6つの座標を変数とする波動関数ψ(x1,y1,z1,x2,y2,z2)の二乗、|ψ(x1,y1,z1,x2,y2,z2)|2 で表されることになる。 |
| ↑4 | もし空間内に粒子が存在しないような条件があれば100%じゃないのでは?…と思う方がひょっとするといるかもしれない。しかし、ここでは「ある粒子」の運動について、粒子が存在する場合のことを考えているわけなので、粒子がどこにも存在しない場合というのは考える必要がない。それに、粒子が存在しないのなら運動について考える必要もないだろう。 |
| ↑5 | 一般には座標は粒子1個とは限らないので、波動関数は系を構成する粒子の個数分の座標の関数ということになるので(x1,y1,z1,…)と表記した。 |
| ↑6 | 左辺では |