ボーアの量子条件
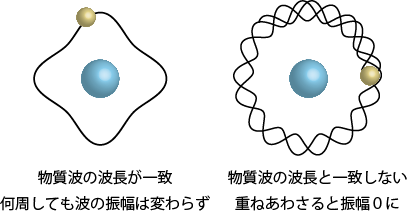
物質波の考え方を使うと原子内の電子のエネルギーが飛び飛びの値となって、原子スペクトルが連続でないことを説明しやすくなる。物質波は波なので、ある波長を持つだけでなく、重ね合わせの性質*1複数の波が存在するとき、その振幅はそれぞれの波の振幅を足し合わせることで表すことができる性質のこと。振幅がF(x,t)という波とG(x,t)という波が同時に空間に存在するとき、その振幅はF(x,t)+G(x,t)となる性質。も持っている。もし電子が原子核を周回するときの1周の長さが物質波の波長と違っていると、回るたびに波を重ね合わされた結果、何周も何周も回った後に振幅がゼロになる。光の強さが波の振幅であるとともに光子の個数にも対応していたのと同じように、物質波の振幅も粒子の個数に対応することになるので、振幅が0だと粒子がどこにも存在できないということになってしまう。一方、1周期の長さが物質波の波長の整数倍ならば波が打ち消されることはないので電子も存在できるので、物質波の波長と電子が周回するときの1周の長さは一致しなければいけない。
というわけで、電子が周回する1周の長さ 2πr と物質波の波長 λ の関係は$$2\pi r=n\lambda\quad(n=1,2,3,…)\quad\rightarrow\quad\lambda=2\pi r/n\tag{1.3.1}$$となる。
これに物質波の波長と速さの関係 λ=h/mv (1.2.6) を使うことで、$$m_e vr=\frac{h}{2\pi}\times n \quad(n=1,2,…)\tag{1.3.2}$$という式が得られる。これはボーアの量子条件と呼ばれ、原子内の電子の運動量がとびとびの値をとらなければいけない(量子化される)ことを意味する。
高校の教科書にも載っているように、これと遠心力とクーロンの法則のつりあいの式から、水素原子のスペクトルの式も再現することができる。
シュレディンガー方程式
ここまで述べてきたように、原子や電子の性質を説明をするにはこれらを粒子として考えるだけではなく、波としての性質を取り入れなければ説明することができない。その説明方法の1つが粒子の運動に物質波として波の性質を取り入れたボーアの量子条件であったが、それでも説明できない原子の性質がまだまだあった。それゆえ、もっと一貫性を持ち普遍的な新しい理論が模索され、量子力学が形作られていった。
現在、量子力学の基本方程式として広く使用されているのはシュレディンガー方程式(シュレディンガーの波動方程式)と呼ばれるものである。シュレディンガー方程式もまた、波の性質と粒子の性質の両方をとりいれることで作られた式になっている。ここからはシュレディンガー方程式がどのようにして形作られてできたものか、古典論の波の式から順を追って紹介することにする。
波が満たす式
古典力学において、波を表す式は波動方程式と呼ばれ、1次元だと$$\frac{\partial^2}{\partial t^2}\psi(x,t)=u^2\frac{\partial^2}{\partial x^2}\psi(x,t)\tag{1.3.3}$$と表される。∂ はディーと呼ばれる偏微分の記号で、多変数の関数(上記の場合、関数 Ψ は x と t の関数)の他の変数を定数と考えて微分するときの記号である。
さて、この波動方程式は電磁波や音波など、波にまつわる様々な現象で成り立つ式である。
たとえば電磁波として$$E(t,x)=\sin\left(2\pi\left(\frac x\lambda-\nu t\right)\right)\tag{1.3.4}$$という電場を考え、実際に波動方程式(1.3.3)の偏微分を計算してみると、両辺は$$\begin{align}左辺&:\partial^2 E(t,x)/\partial t^2=-(2\pi\nu)^2\sin\left(2\pi\left(\frac x\lambda-\nu t\right)\right)\tag{1.3.5} \\ 右辺&:\partial^2 E(t,x)/\partial x^2=-(2\pi/\lambda)^2\sin\left(2\pi\left(\frac x\lambda-\nu t\right)\right)\tag{1.3.6}\end{align}$$ となり、2πν=2π/λから左辺と右辺が等しいことが分かる。
cos, sinを使わず、波としてオイラーの式(0.1.1)を使った複素関数$$E(t,x)=E_0 e^{2\pi i\left(\frac x\lambda-\nu t\right)}$$を考えた場合も、やはり$$\begin{align}左辺&:\partial^2 E(t,x)/\partial t^2=-(2\pi\nu)^2 E_0 e^{2\pi i\left(\frac x\lambda-\nu t\right)}\tag{1.3.7} \\ 右辺&:\partial^2 E(t,x)/\partial x^2=-(2\pi/\lambda)^2 E_0 e^{2\pi i\left(\frac x\lambda-\nu t\right)}\tag{1.3.8}\end{align}$$なので、2πν=2π/λより左辺=右辺となってやはり一致する。
波の式への粒子性の導入と運動量
ここで、上の波動方程式を満たすような波の式に粒子性を表す式を導入することで量子力学の基本式を得ることができる。
簡単のために1次元(x方向)のみを考えると、x 方向に進む波としては以下のような式が考えられる。$$\psi(t,x)=A e^{2\pi i\left(\frac x\lambda-\nu t\right)}\tag{1.3.9}$$ ここに、粒子性として物質波の式(1.2.6)とエネルギーの式(1.2.3より)、$$mv=p=\frac{h}{\lambda} \quad\rightarrow\quad \frac{1}{\lambda}=\frac{p}{h}$$ $$E=h\nu \quad\rightarrow\quad \nu=\frac{E}{h}\tag{1.3.10}$$を導入すると、$$\psi(x,t)=A e^{\frac{2\pi i}{h} \left(px-Et\right)}\tag{1.3.11}$$
となる。
ここで、この式(1.3.11)を時間 t について偏微分すると、$$\frac{\partial}{\partial t}\psi(x,t)=-\frac{2\pi iE}{h} A e^{\frac{2\pi i}{h} \left(px-Et\right)}\tag{1.3.12}$$ $$\rightarrow\quad \frac{ih}{2\pi} \frac{\partial}{\partial t}\psi(x,t)=E\psi(x,t)\tag{1.3.13}$$となる。
また、式(1.3.11)を位置 x について2回偏微分した場合は、
$$\frac{\partial^2}{\partial x^2}\psi(x,t)=\frac{-4\pi^2 p^2}{h^2} A e^{\frac{2\pi i}{h} \left(px-Et\right)}\tag{1.3.14}$$ $$\rightarrow\quad -\frac{h^2}{4\pi^2}\frac{\partial^2}{\partial x^2}\psi(x,t)=p^2 \psi(x,t)\tag{1.3.15}$$となる。
このようにして出てきた式を見てみると、$$p^2\rightarrow-\frac{h^2}{4\pi^2}\frac{\partial^2}{\partial x^2}\tag{1.3.16}$$という対応関係がありそうなことに気づくだろう。とはいえ、この関係の右側は微分の記号なので本来等号が成り立つようなものではない。しかし、この関係から出てくる、
という関係を使い、運動方程式の中の運動量成分を微分係数が入った右辺の形に置き換えるという操作を行って計算を行うと、それまでうまく説明できなかった自然現象をうまく説明できるのみならず、計算結果もちゃんと観測事実と合致するという結果が得られるのである。それゆえ量子力学では、この運動量の対応関係も基本原理に組み込まれている。
時間に依存するシュレディンガー方程式
ここで、質量 m のある粒子がその位置に応じて位置エネルギー(ポテンシャルエネルギー) V(x) をもつとき、全エネルギーは$$E=\frac{1}{2}mv^2+V(x)\tag{1.3.18}$$となる。この式の運動量 mv を p と書き換え、先ほど出てきた波の式 ψ(x,t) を右から掛ける。$$E=\frac{p^2}{2m}+V(x)$$ $$\rightarrow E\psi(x,t)=\frac{p^2}{2m}\psi(x,t)+V(x)\psi(x,t)\tag{1.3.19}$$さらに(1.3.13)の式と、(1.3.15)式もしくは運動量の対応関係(1.3.17)を代入して最終的に出てくるのが次の式。$$\frac{ih}{2\pi}\frac{\partial}{\partial t}\psi(x,t)-\frac{h^2}{8\pi^2 m}\frac{\partial^2}{\partial x^2}\psi(x,t)+V(x)\psi(x,t)\tag{1.3.20}$$ これが「時間に依存するシュレディンガー方程式」として実際に量子力学の基本式として利用されている式の1次元版である。
実際には物質は3つの方向( x,y,z )を持つ3次元空間に存在するので、$$\frac{ih}{2\pi}\frac\partial{\partial t}\psi(x,y,z,t)=-\frac{h^2}{8\pi^2m}\left(\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}+\frac{\partial^2}{\partial z^2}\right)\psi(x,y,z,t)+V(x,y,z)\psi(x,y,z,t)\tag{1.3.21}$$もしくはラプラス演算子$$\Delta=\nabla^2=\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}+\frac{\partial^2}{\partial z^2}\tag{1.3.22}$$を使って書いた
が3次元空間における、ある粒子の時間に依存するシュレディンガー方程式である。
ここまでで見てきたように、波の式と物質波の式、全エネルギーの式などを前提条件とすると、運動量の対応関係 ![]() (1.3.17) と時間に依存するシュレディンガー方程式が出てくることを本節では示したが、今日の量子力学はむしろこの2つの式のほうを基本原理、前提条件として考え、様々な観測量をそれを元に計算していくという形になっている。次節では上記2つの条件を含む量子力学の基本的な原則について紹介を行う。
(1.3.17) と時間に依存するシュレディンガー方程式が出てくることを本節では示したが、今日の量子力学はむしろこの2つの式のほうを基本原理、前提条件として考え、様々な観測量をそれを元に計算していくという形になっている。次節では上記2つの条件を含む量子力学の基本的な原則について紹介を行う。
| ↑1 | 複数の波が存在するとき、その振幅はそれぞれの波の振幅を足し合わせることで表すことができる性質のこと。振幅がF(x,t)という波とG(x,t)という波が同時に空間に存在するとき、その振幅はF(x,t)+G(x,t)となる性質。 |
|---|